48 это идеальный ответ
Чтобы привести многочлен к стандартному виду, нужно:
Привести каждый одночлен многочлена к стандартному виду.
Выполнить приведение подобных одночленов.
Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в его запись.
1) 8ху⁴х³-9х³уу⁷+10zz⁵= 8х¹⁺³у⁴ - 9 х³у¹⁺⁷ +10 z¹⁺⁵= 8x⁴y⁴ -9x³y⁸+10z⁶
найдем степень многочлена :
8x⁴y⁴ : 4+4=8
9x³y⁸: 3+8= 11
10z⁶ : 6
Наибольшая степень 11 - это и будет степенью многочлена
2) 0,2а⁵bb⁶ - 1,1xyx⁷+k⁸t²k= 0,2a⁵b⁷ - 1.1x⁸y +k⁹t²
найдем степень многочлена :
5+7= 12
8+1=9
9+2= 11
Наибольшая степень 12 - это и есть степень многочлена
3)
найдем наибольшую степень :
2+5= 7
8+10=18
16+8=24
Степень многочлена - 24
4)
найдем наибольшую степень :
10+3=13
8+8=16
10
Степень многочлена - 16
Объяснение:
1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:
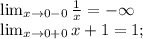
Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).
Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как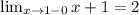 
При x=1 ⇒y=2.
Подставим координаты (1;2) в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: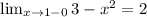 
Действительно 2=2, значит функция не будет являться непрерывной в точке 1.
ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1
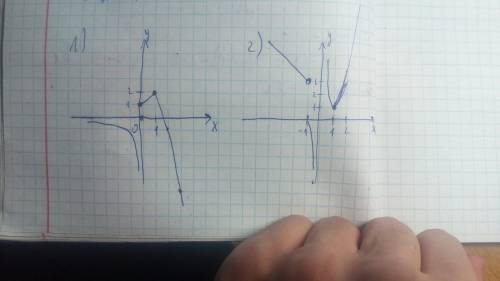
2) Аналогично:
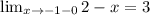
3≠-1, значит -1- это точка разрыва.
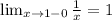
В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.
Проверим: 
.
Так как точка х=0 лежит в области определения функции 
, а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
ответ: х=-1 - точка разрыва, х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1
3) 48 вот этот правильный ответ