Если фотографий меньше ста, то печать одной фотографии в ателье стоит 3 руб. 50 коп., а если фотографий 100 или больше, то печать одной фотографии стоит 3 руб. например, выгоднее отдать в печать 100 фотографий по 3 руб., чем 99 по 3,5 руб. при каком наименьшем числе фотографий можно добавить еще несколько фотографий до сотни, чтобы после этого плата за печать уменьшилась? 2. время (1 ). самолет вылетает из москвы в 12: 00, а прилетает в бишкек в 18: 00. обратно самолет вылетает в 8: 00, а прилетает в 10: 00. сколько времени длится полет? время указывается местное. 3. борцы (1 ). есть 9 борцов разной силы. в поединке любых двух из них всегда побеждает сильнейший. можно ли разбить их на три команды по три борца в каждой так, чтобы во встречах команд по системе «каждый с каждым» (9 поединков для двух команд) первая команда по числу побед одержала верх над второй, вторая – над третьей, а третья – над первой? (пусть номер борца означает его силу). 4. мобильник (1 ). заряженный мобильный телефон полностью разряжается за 6 ч разговора или за 210 ч покоя во включенном состоянии. человек ехал на поезде с включенным телефоном, причем половину времени в пути разговаривал по телефону. за время поездки полностью заряженный телефон полностью разрядился к концу пути. сколько времени продолжалась поездка? 5. зарплата (2 ). у вани 10 сотрудников с неравными зарплатами. каждый месяц ваня повышает зарплату 9-и из них (кому захочет) на 1 рубль. докажите, что ваня сможет таким сделать все зарплаты равными. (зарплата – целое число рублей.) 6. школа (2 ). сёла a, b и c расположены в вершинах равностороннего треугольника. в селе a живут 100 школьников, в селе b - 200, а в селе c - 300. где нужно построить школу, чтобы суммарное расстояние, проходимое всеми школьниками, было бы как можно меньше? 7. кокосы (3 ). у мартышки было 3 кокосовых ореха. один из них упал с 16 этажа и разбился. как мартышке за 5 попыток определить, начиная с какого этажа, орехи при падении будут разбиваться, если у нее осталось только 2 ореха? (если орех не разбился, то его можно использовать еще раз). 8. выходные (3 ). в мексике каждый автомобиль хотя бы день в неделю не должен ездить (владелец сообщает полиции номер автомобиля и «выходной» день недели этого автомобиля). в некоторой семье все взрослые желают ездить ежедневно (каждый – по своим делам). какое наименьшее число автомобилей должно быть в семье, если взрослых в ней 8 человек? 9. кубик (3 ). из единичных кубиков составлен кубик размером 4 × 4 × 4. какое наибольшее число кубиков можно из него удалить так, чтобы при взгляде на оставшуюся фигуру с любой из шести возможных сторон был виден квадрат со стороной 4 без просветов? ( пример и объяснить, почему больше быть не может.)
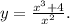
1.)
100 фотографий по 3 рубля = 300 рублей...
(100-x) фотографий по 3,5 рубля = 350 - 3,5X > 300
3.5X < 50
X < 50/3.5 = 14.28...
x=14