Объяснение:
1) (x+2)²(x-5)^3=(x-5)(x+2)^4
(x+2)²(x-5)^3-(x-5)(x+2)^4=0
(x+2)²(x-5)((x-5)²-(x+2)²)=0
(x+2)²(x-5)((x-5-(x+2))((x-5+(x+2))=0
(x+2)²(x-5)·(-7)(2x-3)=0
-14(x+2)²(x-5)(x-1,5)=0
(x+2)²(x-5)(x-1,5)=0
x= -2; 1,5; 5;
ответ: -2; 1,5; 5;
2) (2x+1)^3(2x-3)^5=(2x+1)^5(2x-3)^3
(2x+1)^3(2x-3)^5-(2x+1)^5(2x-3)^3=0
(2x+1)^3(2x-3)^3((2x-3)^2-(2x+1)^2)=0
(2x+1)^3(2x-3)^3((2x-3)-(2x+1))((2x-3)+(2x+1))=0
(2x+1)^3(2x-3)^3·(-4)(4х-2)=0
-16· (2x+1)^3(2x-3)^3(х-0,5)=0
(2x+1)^3(2x-3)^3(х-0,5)=0
8·8(x+0,5)^3(x-1,5)^3(х-0,5)=0
(x+0,5)^3(x-1,5)^3(х-0,5)=0
х= -0,5; 0,5; 1,5;
ответ:-0,5; 0,5; 1,5;
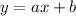 - a угловой коэффициент,b точка пересечения прямой с осью у.
- a угловой коэффициент,b точка пересечения прямой с осью у. , следовательно, данные прямые пересекают ось у в начале координат.
, следовательно, данные прямые пересекают ось у в начале координат.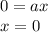
 - область определения.
- область определения.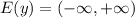 - область значений.
- область значений.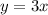
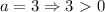 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.

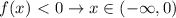

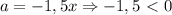 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)

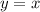
 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)


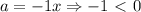 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)

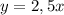
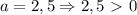 , следовательно, данная функция всегда возрастает.
, следовательно, данная функция всегда возрастает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)


 следовательно, данная функция всегда убывает.
следовательно, данная функция всегда убывает.
![f(x) \geq 0 \rightarrow x\in(-\infty,0]](/tpl/images/0317/3972/042d5.png)




В ромбе все стороны равны, значит, одна сторона равна 9. Если тупой угол 120, то острый угол равен 180-120=60 градусов. Если проведем меньшую диагональ, то она образует равнобедренный треугольник со сторонами этого ромба(т.к. стороны ромба равны). Угол в этом равнобедренном треугольнике равен 60 градусов, значит, он равносторонний. Значит, меньшая диагональ равна стороне ромба, т.е. 9.
ответ:9