
Объяснение:
{ x² - y² = 4 , ⇒ { x² - y² = 4 , ⇒ { x² - y² = 4 , ⇒
{ x⁴ - y⁴ = 64 ; { (x² - y²)(x² + y²) = 64 ; { 4(x²+ y²) = 64 ;
{ x² - y² = 4 ,
{ x²+ y² = 16 ; додаємо рівняння системи :
2x² = 20 ; > x² = 10 ; > x₁,₂ = ± √10 . При таких
значеннях х із ІІ - го рівняння останньої системи маємо :
10 + у² = 16 ; > у² = 16 - 10 ; > у² = 6 ; > y₁,₂ = ± √6 .
Отже , x²+ y² = 16 ; а розв"язки системи такі :
(- √10 ;- √6 ) , (- √10 ; √6 ) , ( √10 ;- √6 ) , ( √10 ; √6 ) .
Система рівнянь має 4 розв"язки .
7/12
Объяснение:
Заштрихованная фигура состоит из двух криволинейных трапеций. Одна, находящаяся над осью абсцисс, ограничена графиком y = x², двумя вертикальными прямыми x = -1 и x = 0, а также самой осью Ox. Вторая, находящаяся под осью абсцисс (из-за этого ее площадь возьмем со знаком минус), ограничена графиком y = x³, теми же вертикальными прямыми и той же осью Ox.
Тогда площадь S рассматриваемой фигуры будет равна сумме двух определенных интегралов (один — от x², другой — от x³ со знаком минус), оба вычисленных на отрезке [-1; 0]:
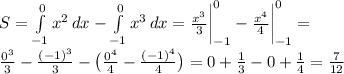

ответ:надеюсь
Объяснение: