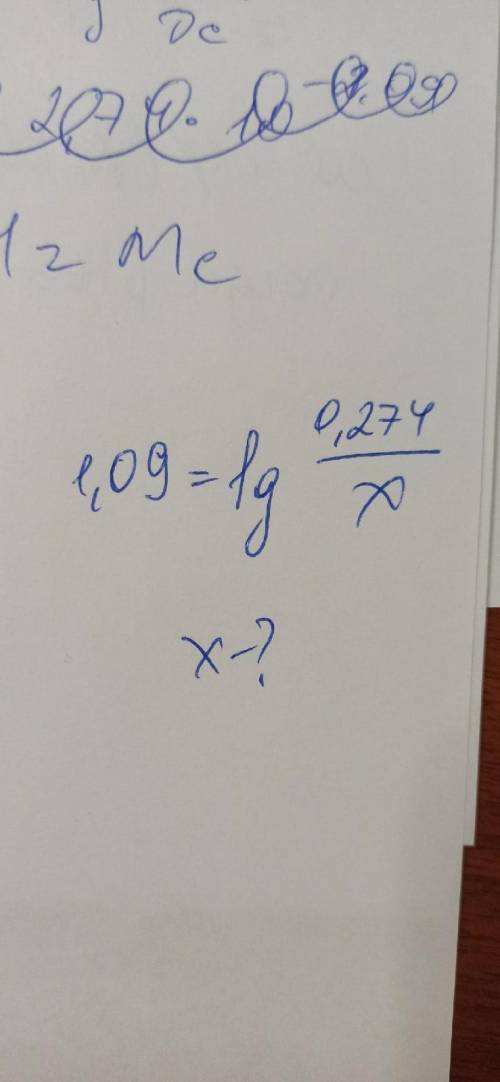
ответ: по течению - 20 км/ч, против течения - 16 км/час.
Объяснение: пусть х - собст. скорость лодки, у - скорость течения. За 2 часа по течению лодка пройдет 2(х + у) км, а за 5 часов против течения - 5(х - у) км. Так как вместе она проплыла 120 км, имеем первое уравнение: 2(х+у) + 5(х - у) = 120.
За 7 часов против течения лодка проплыла 7(х - у) км, за 3 часа по течению - 3(х + у) км. Так как 7(х - у) больше чем 3(х + у) на 52, имеем второе уравнение: 7(х - у) - 52 = 3(х + у).
Объединяем оба уравнения в систему (см. ниже). Решая ее, получаем: х = 18 - собст. ск. л., у = 2 - ск. теч. реки. Тогда скорость по течению реки равна 18 + 2 = 20(км/ч), а против течения - 18 - 2 = 16(км/ч).
По теореме синусов:
a : sin 45° = c : sin 30°
a = c · √2/2 : (1/2) = c√2
b : sin 105° = c : sin 30°
Найдем sin 105° :
sin 105° = sin (90° + 15°) = cos 15°
cos 15 = cos( \frac{30}{2} ) = \sqrt{ \frac{cos 30 + 1}{2} } = \sqrt{ \frac{ \sqrt{3}+2 }{4} } = \frac{1}{2} \sqrt{ \frac{4+2 \sqrt{3} }{ 2 } }
cos15= \frac{1}{2} \sqrt{ \frac{ ( \sqrt{3}+1 )^{2} }{2} } = \frac{ \sqrt{3}+1 }{2 \sqrt{2} }
b = c · sin105° : sin 30° = 2c · 1/2 · (√3 + 1)/√2 = c · (√3 + 1)/√2
m² = (b² + c²)/2 - a²/4
m² = (c · (√3 + 1)/√2)²/2 + c²/2 - 2c²/4 = c²(√3 + 1)²/4
m = c · (√3 + 1)/2 = b/√2
По теореме синусов из ΔАМС:
m : sin 30° = b : sinα
sinα = 1/2 · b / m = b/(2m) = b / (2 · b/√2) = √2/2
Так как α тупой угол, α = 135°