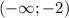
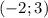(рис. 2)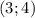
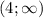
Объяснение: пусть скорость катера=х, и если он по течению, то его скорость увеличилась на 3км/ч, поэтому по течению он проплыл 48км со скоростью х+3. Когда он плыл против течения, то скорость течения ему не а наоборот и он проплыл 18км со скоростью х-3. По течению он потратил 48/х+3 времени, а против 18/х-3. Зная, что он потратил на всю дорогу 3 часа, составим уравнение:
(48/х+3)+(18/х-3)=3 |на этом этапе подбираем общий знаменатель:
(48х-144+18х+54)/(х+3)(х-3)=3
(66х-90)/(х²-9)=3 | перемножим числитель и знаменатель соседних дробей крест накрест:
(х²-9)3=66х-90
3х²-27-66х+90=0
3х²-66х+63=0 |÷3
х²-22х+21=0
Д=484-4×21=484-84=400
х1=(22-20)/2=2/2=1
х2=(22+20)/2=42/2=21
Итак: есть 2 варианта значения х, но первый вариант нам не подходит поскольку скорость катера на самом деле больше, чем 1км/ч, поэтому используем х2=21.
Скорость катера=21км/ч
Обозначьте 2^x = а и 2^y = b.
Первое уравнение перепишется в виде b = 24 - 4a
Второе уравнение перепишется в виде b = 49 - 2a^2
Тогда 24 - 4a = 49 - 2a^2, откуда а = 4 (корень подходит) и а = -2 (корень не подходит)
Вернувшись к обозначениям, получим: х = 2.
Тогда b = 24 - 4*4 = 8.
Вернувшись к обозначениям, получим: y = 3.
ответ: (2;3)