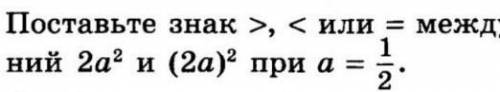
В решении.
Объяснение:
Дана функция y=x²-9. Построй график функции y=x²-9 .
График - парабола, ветви направлены вверх.
Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу.
Таблица:
х -4 -3 -2 -1 0 1 2 3 4
у 7 0 -5 -8 -9 -8 -5 0 7
a) координаты вершины параболы: (0; -9)
х₀= -b/2а= 0/2= 0;
у₀= 0²-9= -9.
б) при каких значениях аргумента значения функции отрицательны?
Смотрим на график, у<0 при х от -3 до 3, то есть, х∈(-3, 3).
в) при каких значениях аргумента функция возрастает?
Согласно графика [0; +∞ ) .
г) при каких значениях аргумента Функция убывает?
Согласно графика (-∞, 0].
1) Один раствор имеет x кг кислоты, а второй y кг.
Если мы смешаем 100 кг одного раствора и 85 кг другого, то получим 185 кг раствора концентрацией 44%, то есть в них содержится
185*0,44 = 81,4 кг кислоты.
x + y = 81,4
Если смешать одинаковые массы, например, по 1 кг, получится 47%
x/100 + y/85 = 0,47*2 = 0,94
Подставляем 1 уравнение во 2 уравнение.
x/100 + (81,4 - x)/85 = 94/100
(81,4 - x)/85 = (94 - x)/100
100(81,4 - x) = 85(94 - x)
8140 - 100x = 7990 - 85x
150 = 15x
x = 150/15 = 10 кг на 100 кг раствора, то есть концентрация 10%.
y = 81,4 - x = 81,4 - 10 = 71,4 кг на 85 кг раствора, концентрация 84%
ответ: в 1 сосуде содержится 10 кг кислоты.
2) Решается точно также.
Если мы смешаем 50 кг одного раствора и 20 кг другого, то получим 70 кг раствора концентрацией 14%, то есть в них содержится
70*0,14 = 9,8 кг кислоты.
x + y = 9,8
Если смешать одинаковые массы, например, по 1 кг, получится 23%
x/50 + y/20 = 0,23*2 = 0,46
Подставляем 1 уравнение во 2 уравнение.
x/50 + (9,8 - x)/20 = 46/100
2x/100 + 5(9,8 - x)/100 = 46/100
2x + 5*9,8 - 5x = 46
49 - 46 = 5x - 2x
3 = 3x
x = 1 кг на 50 кг раствора, это концентрация 2%.
y = 9,8 - 1 = 8,8 кг на 20 кг раствора, концентрация 44%
ответ: В 1 сосуде содержится 1 кг кислоты.
знак будет меньше так как в первом случае мы возводим в квадрат 1/2 и это равно 1/4 из чего следует что 2*1/4= 1/2