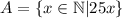
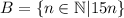
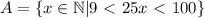
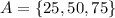
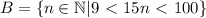
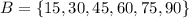
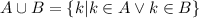 - то есть, это такое множество всех k, так что, либо k в А либо в В, или в А и в В одновременно.
- то есть, это такое множество всех k, так что, либо k в А либо в В, или в А и в В одновременно.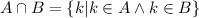 - то есть, это такое множество всех k, так что, k и в А и в В одновременно.
- то есть, это такое множество всех k, так что, k и в А и в В одновременно.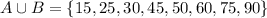 - то есть, это множество всех чисел которые кратны либо 25 либо 15, или 25 и 15 одновременно.
- то есть, это множество всех чисел которые кратны либо 25 либо 15, или 25 и 15 одновременно.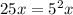
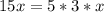

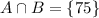
для начала нам нужно написать само ур-е касательной, потом найти значение х( правый верхний угол), х подставить в первоначальное ур-е(корень из х), найти производную, подставить значение х в производную....