1. Найдите производную функции y =4x3 1) 12x2 2) 12x 3) 4х24) 12х3
2. Найдите производную функции y =6.х - 11
1) -5 2) 11 3) 64) бх
х
х* 2)
3. Найдите производную функции
1
х- 1
2x+1 1
1)
2
3)
х
4)
4. Найдите производную функции y=xsin x
1) sin x- xcos x 2) sin x+x cos x 3) cos x 4) x+x cos x
y=x' + sin x в точке x =л
5. Найдите производную функции
1) л' - 12) 2л +13) 2л - 1 4) 2л
3х?
+2х
2
B
2
6. Вычислите значение производной функции
точке хо=2.
1) 10 2) 12 3) 8 4) 6
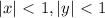
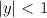 возвести в квадрат, получив,
возвести в квадрат, получив, 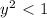 , что и требовалось проверить.
, что и требовалось проверить.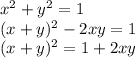
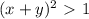
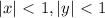 , следует, что 0 <x < 1, 0 < y < 1
, следует, что 0 <x < 1, 0 < y < 1
И ещё одна тонкость встречается в тех случаях, когда Вы получаете неравенства, содержащие множитель 0 перед переменной после упрощения частей неравенства.
Неравенство 0·х < 0 не имеет решений, а решением неравенства 0·х > - 8 является любое действительное число.
В подобных случаях нужно внимательно оценивать левую и правую части, делать выводы.
Привожу примеры решения двух линейных неравенств: