Окей, я просто построю тебе эти два графика.
Ладно, объясню.1) 5х+4у=10 надо сделать так, чтобы с одной стороны был у
4у=10-5х потом обе части уравнения делим на 4
у=(10-5х):4 теперь составим таблицу с двумя значениями х
х 0 2 у(0)=(10-5*0):4=10:4=2,5
у 2,5 0 у(2)=(10-5*2):4=0:4=0
2) 5х-3у=3 надо сделать так, чтобы с одной стороны был у
3у=-3+5х потом обе части уравнения делим на 3
у=-1+1 2/3х теперь составим таблицу с двумя значениями х
1 2/3 значит одна целая две третьих.
х 0 2 у(0)=-1+1 2/3*0=-1
у -1 2 1/3 у(2)=-1+1 2/3*2=7/3=2 1/3
ну, теперь начертим график
там не очень хорошо видно, но точка пересечения (6/5;1)
Держи!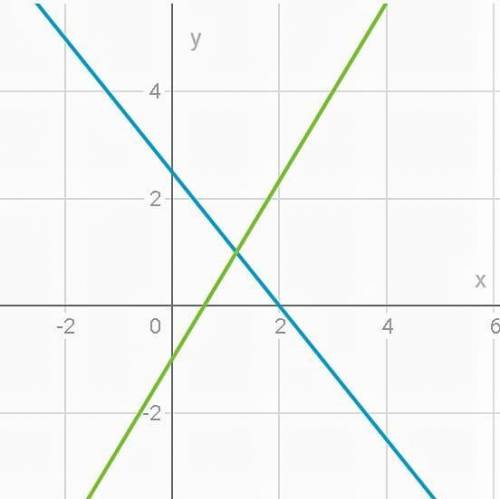
Формулы общего вида(1) Формула понижения nй четной степени синусаsin^n(\alpha) = \frac{C_{\frac{n}{2}}^{n}}{2^n} + \frac{1}{2^{n-1}} \sum_{k=0}^{\frac{n}{2}-1} (-1)^{\frac{n}{2}-k} C_{k}^{n}cos((n-2k)\alpha)sinn(α)=2nC2nn+2n−11∑k=02n−1(−1)2n−kCkncos((n−2k)α)(2) Формула понижения nй четной степени косинусаcos^n(\alpha) = \frac{C_{\frac{n}{2}}^{n}}{2^n} + \frac{1}{2^{n-1}} \sum_{k=0}^{\frac{n}{2}-1} C_{k}^{n}cos((n-2k)\alpha)cosn(α)=2nC2nn+2n−11∑k=02n−1Ckncos((n−2k)α)(3) Формула понижения nй нечетной степени синусаsin^n(\alpha) = \frac{1}{2^{n-1}} \sum_{k=0}^{\frac{n-1}{2}} (-1)^{\frac{n-1}{2}-k} C_{k}^{n}sin((n-2k)\alpha)sinn(α)=2n−11∑k=02n−1(−1)2n−1−kCknsin((n−2k)α)(4) Формула понижения nй нечетной степени косинусаcos^n(\alpha) = \frac{1}{2^{n-1}} \sum_{k=0}^{\frac{n-1}{2}} C_{k}^{n}cos((n-2k)\alpha)cosn(α)=2n−11∑k=02n−1Ckncos((n−2k)α)