Вход
Регистрация
Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
.....больше.....
..меньше..
vall331ukrnet
11.11.2022 03:46 •
Алгебра
Упростить выражение cos35°+cos25°
НЕ С ИНТЕРНЕТА
👇
Увидеть ответ
Ответ:
gavrilindan
11.11.2022
ответ: cos35°+cos25°=2cos
cos
=2cos30°cos5°=√3*cos5°
Объяснение:
4,5
(64 оценок)
Ответ:
marinedzhan000
11.11.2022
Для упрощения данного выражения нам понадобится знание о тригонометрических формулах суммы углов.
Заметим, что у нас даны две суммы косинусов - cos35° и cos25°. Мы можем использовать тригонометрическую формулу суммы двух углов, которая гласит:
cos(x + y) = cos(x)*cos(y) - sin(x)*sin(y),
где x и y - углы.
Применим данную формулу к нашим углам 35° и 25°:
cos(35° + 25°) = cos(35°)*cos(25°) - sin(35°)*sin(25°).
Так как нам нужно найти cos35° + cos25°, то рассмотрим только первое слагаемое:
cos(35°)*cos(25°).
Теперь возвращаемся к начальному выражению и подставляем результат:
cos35° + cos25° = cos(35° + 25°) = cos(60°) = 0.5.
Таким образом, упрощенное выражение равно 0.5.
Обоснование:
Мы использовали знание тригонометрической формулы суммы углов, которая позволяет нам упростить данное выражение. Затем мы подставили значения углов и рассчитали результат.
4,6
(58 оценок)
Проверить ответ в нейросети
Это интересно:
З
Здоровье
18.07.2020
Как нормализовать нерегулярный менструальный цикл: практические советы...
К
Компьютеры-и-электроника
17.08.2022
Как сделать сайт в Word: подробное руководство...
К
Кулинария-и-гостеприимство
22.07.2021
Как сделать печенье «Отпечаток»...
К
Кулинария-и-гостеприимство
27.04.2022
Лимонно-медовая вода: не только вкусно, но и полезно...
Д
Дом-и-сад
08.12.2021
Как сделать печь для плавки металла...
М
Мир-работы
05.04.2023
Как пережить увольнение: советы профессионалов...
Д
Дом-и-сад
27.10.2021
Как найти распределительный щиток или блок предохранителей...
К
Компьютеры-и-электроника
28.03.2021
Как удалить историю веб поиска в Google: простые шаги для защиты вашей конфиденциальности...
К
Компьютеры-и-электроника
27.03.2021
Как поймать Суикуна в игре Покемон - Кристальная версия...
О
Образование-и-коммуникации
07.08.2020
Как нарисовать собачью морду: советы и инструкции...
Новые ответы от MOGZ: Алгебра
sasapanskov
27.09.2021
Решить графическое уравнение -x*2=4x...
pavlov0202
27.09.2021
Найти предел последовательности...
сич23
10.02.2022
По данному рисунку выпишите а) все хорды б) все радиусы Найдите: радиус окружности если KH=15 ...
nastiamakeeva0
09.11.2021
Скоротить дріб 4ікс в квадраті плюс ікс мінус 3 дріб ікс в квадраті мінус 1...
anyta141006
15.10.2021
Постройте графики функуии и укажите свойства ; y=| x-3 y=4/(x-2) (Толька график)...
ulzhalgasamangEldy
29.05.2020
1. Решить систему уравнений: 1) 3х + у = 1 2) -5х + 4у = -2 2х – 3у = 8 3х + 7у = -27 2. Первый рабочий работал 7 дней, а второй – 9 дней. Вместе они изготовили 174 детали. Сколько...
egekaterina201
20.10.2022
Алёу, народ, математики, хэлп! Запишите уравнение касательной к графику функции! f(x) = 2√x+x в точке х0=1...
gabpara007
31.07.2021
Внесите вынесите в{ из-под знак(а) корня ...
dania45451
16.07.2021
1. В арифметичній прогресії a5=14,91 a9=20,11. Обчислити a1. 2. Обчислити суму перших п ятнадцяти непарних чисел. 3. Одним із мобільних операторів було запропоновано акцію «Довше розмовляєш...
asyast26
10.11.2020
Используя данные диаграммы определите на сколько миллионов человек выросла численность городского населения с 2014 по 2017г. 2014-106,6 2015-108,3 2016-108,6 2017-109...
MOGZ ответил
За 4 кг картошки заплатили 88 руб. сколько стоят 13 кг картошки? (составь пропорцию...
Напишите одноименные названия городов и рек россии . пример: р. волга - г. волгоград...
Выберите правильные ответ и поясните его.если вы хотите нырнуть на длительное время,то...
Произведение отцы и дети. тургенев. кленовый лист, когда падает на землю, похож...
Аккумулятор, емкость которого равна q = 20 а-ч, заряжают выпрямленным синусоидальным...
нужно выписать слова с арфограмами...
До завтра 7 класс 2 четверть сор2 по только 3,4 ....
Le livre francais во множественном числе...
6.5.2.1 in three minutes, say or write as many true sentences as you can using the...
Потрібно скласти 7 речень із словами...
Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ
Оформи подписку
О НАС
О нас
Блог
Условия пользования
Авторское право
Политика конфиденциальности
Предпочтения cookie-файлов
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
App
Вход
Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ
ответ: cos35°+cos25°=2cos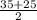 cos
cos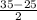 =2cos30°cos5°=√3*cos5°
=2cos30°cos5°=√3*cos5°
Объяснение: