1) 18 + 2 = 20 км/ч скорость катера по течению
2) 240 : 20 = 12 часов шёл катер по течению
3) 18 - 2 = 16 км/ч скорость катера против течения
4)0 240 : 16 = 15 часов шёл катер против течения
5) 12 +15 = 27 часов время в пути
6) 240 х 2 = 480 км всё расстояние,котрое катер
7) 480 : 27 =17,8 км/ч средняя скорость катера на всём пути.
1. 2)
2. 3)
Объяснение:
1. 
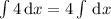, интеграл 
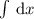табличный и равняется 
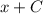, тогда исходный равняется 
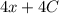, произведение констант — тоже константа, поэтому решением будет 
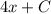, что соответствует второму варианту ответа.
2. Область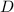 
, ограниченная указанными кривыми 
, 
, 
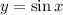и 
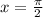, показана на приложенном рисунке. Получается, что 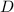задают два неравенства, 
и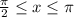 
. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.
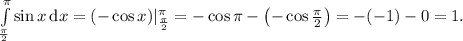
(Так получается, ибо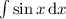 
— табличный интеграл, равный 
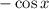, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть 
, при известном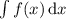 
, то есть 
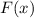, притом константа в таком случае игнорируется.)
Полученный результат соответствует третьему варианту ответа.
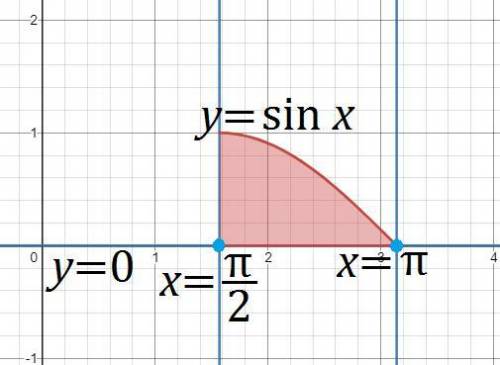
Каждой точке (х; у) графика у = f(x) соответствует единственная точка (х; - у) графика у =- f(x) и наоборот. Точки (х; у) и (х; - у) симметричны относительно оси ОХ. Значит, графики у =f(x) и y = -f(x) симметричны относительно оси ОХ.
Пример 1
Построить график функции у = - .
Решение
Строим график функции у = , а затем строим симметрично относительно оси ОХ.
Симметрия относительно оси ОУ (оси ординат)
Каждой точке (х; у) графика у = f(x) соответствует единственная точка (-х; у) графика у = f(-x), и наоборот. Но точки (х; у) и (-х; у) симметричны относительно оси ОУ, значит, графики у = f(x) и у = f(-x) симметричны относительно оси ОУ.
Пример 2
Построить график функции у = .
Решение
Строим график функции у =, а затем строим симметрично относительно оси ОУ.
Пример 3
Построить график функции у = -
Решение
Выполним ряд последовательных преобразований:
строим график функции у = ;
строим симметрично относительно оси ОУ, т. е. получаем график функции у = ;
строим симметрично относительно оси ОХ, т.е. получаем искомый график функции у = -.
Параллельный перенос (сдвиг) вдоль оси абсцисс
Пусть дан график функции у = f(x).
Чтобы построить график функции у = f(x+a), где а – некоторое данное число, достаточно график функции у= f(x) перенести параллельно направлении оси ОХ на расстояние в положительном направлении, если а<0, и в отрицательном направлении, если а>0.
Пример 4.
Построить графики функций у =(х - 3)² и у =(х + 1)².
Решение
Строим график функции у = х² (пунктиром). Переносим его дважды: в положительном направлении оси ОХ на расстояние, равное 3, и получаем график у = (х – 3)²; в отрицательном направлении оси ОХ на расстояние, равное 1, и получаем график у = (х + 1)².
Параллельный перенос (сдвиг) вдоль оси ординат
Пусть дан график функции у =f(x).
Чтобы построить график функции у = f(x) + a, где а – некоторое данное число, достаточно график функции у = f(x) перенести параллельно оси ОУ на расстояние в положительном направлении, если а >0, и в отрицательном, если а /I>0.
Пример 5.
Построить график функции у = 5+.
Решение
Строим график у = (пунктиром). Переносим его в положительном направлении оси ОХ на расстояние, равное 4, и получаем график у =, а затем переносим в положительном направлении оси ОУ на расстояние, равное 5, получаем искомый график у = 5 +.
найдем общее время в пути
по течению: 240:(18+2)=12
против течения: 240:(18-2)=15
общее время в пути 12+15=27ч
общий километраж пути: 240+240=480
средняя скорость: 480:27=17,8 км/ч