x∈[-4 ; 4]
Объяснение:
Решим каждое неравенство в отдельности:
1) 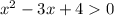
Приравняем к 0, чтобы найти корни уравнения:

Это обычное квадратное уравнение, значит, сначала найдем дискриминант:
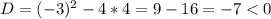
D < 0, а значит, вещественных корней нет.
Значит, неравенство выполняется ВСЕГДА или НИКОГДА. Проверим, подставив любое число в уравнение. Например, x = 10:
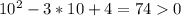
Получили значение больше 0, значит, неравенство выполняется ВСЕГДА при ЛЮБЫХ значениях x
x ∈ (-∞ ; +∞)
2) 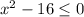
Приравняем к 0 и найдем корни:

Получили 2 корня. Наносим их на координатную ось, ставим 2 точки: -4 и 4. Далее расставляем знаки функции на участках (путем подстановки любого числа из этого участка: до -4 возьмем -10, подставим в уравнение и получим положительное число → +; между -4 и 4 возьмем 0, подставим, получим отрицательное число → –; от 4 и далее возьмем 10 и получим положительное число → +). Нам нужен тот участок, в котором функция принимает ОТРИЦАТЕЛЬНОЕ значение, т.е. там где стоит минус.
Значит ответ: x∈[-4 ; 4]
Скобки квадратные, т.е. неравенство строгое (есть знак равно).
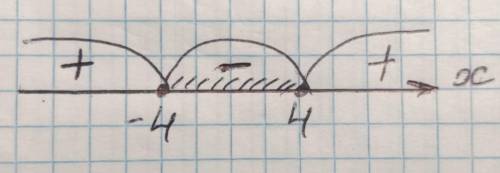
3. мин
е
т
з.м1ш
л
1 + kni
коэффициенты пульсации напряжения и тока связаны между собой в виде
к
л
(8-28)
характер зависимости коэффициентов пульсации друг от друга при разных коэффициентах использования напряжения питания показан на графиках (рис 8-5, б). из этого графика следует, что малые значения коэффициентов пульсации возможны при низком использовании питающего напряжения.
процессы в накопителе при его разряде на нагрузку с импульсом прямоугольной формы описываются исходным уравнением
dl du
е
и
hrz или r
(8-29)
полагая
и
с с
и
и(; --с);
de di
,1 i
после к виду
несложных преобразований исходное уравнение можно
r \
rrh 1 crrii
h7
или
crrn
(8-30)
где обозначено
решение уравнения (3) имеет вид:
i p-at
3. мйн*
r3 +
.-ah.
); 1
з.мин
(1 - n).
зарядный ток г'з оказывается минимальным в момент времени / = о, когда еще только начинается разряд конденсатора, т. е. до начала протекания импульса тока по нагрузке.
при подстановке значения тока и представлении его в относительном масштабе, получим:
(8.31)
а при < 1
л
подставляя значение тока i% в .mi уравнение (и^ -
е - isra) и выражая напряжение в относительном масштабе, можно найти
uq к
1 - (1 - п) е- = j-- (1 -
или при к > > 1
и^ е
(8-32)
во время /== tji-т- г , т. е. в промей< : утках между импульсами тока в нагрузке, конденсатор будет заряжаться и ток заряда будет уменьшаться с ростом напряжения uq на конденсаторе. в эти моменты времени ток через зарядное сопротивление описывается уравнением
ь - сиакс^ - смакс^
где 1 - вpeш, изменяющееся в пределах от до г^. учитывая, что / = ; к ;
смакс =r-j~ = пи -j- . получим
/пи
в 5ти же отрезки времени напряжение иа конденсаторе будет
с = - /з^з = 11 - (1 - пг) е- ].
или
-=1 (1 т)е- . (8-34)
В решении.
Объяснение:
Построить график функции y=x²+6x+5.
Используя график, найдите:
а)f(2); f(6);
б) значения х, при которых f(x)= -3; f(x)= -5;
в) при каких значениях аргумента функция принимает положительные значения, а при каких отрицательные?
г) найти наименьшее и наибольшее значения функции на отрезке [2;5]
График функции - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, занести в таблицу. По вычисленным значениям построить параболу.
Таблица:
х -7 -6 -5 -4 -3 -2 -1 0 1
у 12 5 0 -3 -4 -3 0 5 12
а) Согласно графика, f(2)= 21. Это означает, что в точке графика, где х=2, у=21.
Согласно графика, f(6)= 77. Это означает, что в точке графика, где х=6, у=77.
б) Согласно графика, f(x)= -3 при х= -2; х= -4. Это означает, что в точках графика, где у= -3, х= -2 и х= -4 (график - парабола, ветви две, поэтому значения х два).
Согласно графика, значений х, при которых f(x)= -5 не существует, так как вершина графика (-3, -4), график находится выше у= -4 и нет точек пересечения с осью Ох.
в) Согласно графика, у> 0 при х∈(-∞; -5)∪(-1; +∞), то есть, при х от
- бесконечности до -5 и от -1 до + бесконечности, функция принимает положительные значения, > 0.
Согласно графика, у < 0 при х∈(-5; -1), то есть, при х от -5 до -1, функция принимает отрицательные значения, < 0.
г) Согласно графика, на отрезке [2;5] у наим. = 21; у наиб. = 60.