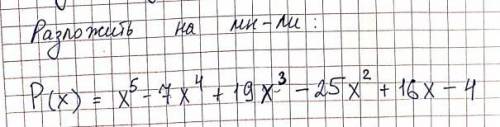
Объяснение:
6.Надо начертить прямую линию. В середине поставить точку 0. Это будет начало координатной прямой и будет =0.
Вправо от нуля -положительные значения, влево от нуля -отрицательные.
От точки 0 вправо отложить 1,5см (точкаР) и 3см (точкаК).
Влево отложить 3см (т. М ), и так как влево идут отрицательные величины поставить под точкой М -3, затем отложить отнуля влево еще 3,5 см , это будет точка N ( -3,5см).
Противоположные точки( точки, равные по модулю) - это точки 3 и -3.
|3|=3 и |-3|=3
7. | -5,2 | + | -8,4 | = 5,2 +8,4 = 13,6
8. a) | x| - 8 = 0
| x| = 8
x = 8; -8
б) - (-x) = -12
x = -12
в) 3 |x| + 1 =10
3 |x| = 9
|x| = 3
x =3; -3
9. ... = 15/2 * |-2/3| + | 6 | : 1/10 = 15/2* 2/3 + 6/10 = 5 +0,6 = 5,6
10. 4 : (2 |x| +4) = 1
4 : (2x+4) = 1
2x + 4 = 4 : 1
2x = 4-4
2x =0
x =0
Объяснение:
Для того, чтобы разложить выражение на множители, приравняем правую часть равенства к нулю:
Слагаемое –4 имеет следующие делители:
Подставим вместо "х" единицу:
Единица обращает уравнение в верное равенство ⇒ один из множителей исходного выражения равен (х – 1). Разделим исходный многочлен на (x – 1):
Теперь разложим многочлен
Приравняем его к нулю:
Слагаемое 4 имеет следующие делители:
Подставим вместо "х" единицу:
Единица обращает уравнение в верное равенство ⇒ один из множителей выражения равен (х – 1). Разделим многочлен на (x – 1):
Теперь разложим многочлен
Приравняем его к нулю:
Слагаемое –4 имеет следующие делители:
Подставим вместо "х" единицу:
Единица обращает уравнение в верное равенство ⇒ один из множителей выражения равен (х – 1). Разделим многочлен на (x – 1):
Теперь разложим многочлен
Это квадрат разности двух выражений:
Выпишем полученные множители:
Отсюда получаем, что