9x2 + 3x; б) 6xy +3x2y – 12xy2
2°. Разложите на множители:
а) y(у – 1) + 2(y – 1); б) x2 – 64.
3°. Сократите дробь (x^2+ 3x)/(3a+ax).
4°. У выражение (а – b)2 – (а – b)(а + b).
5°. Решите уравнение x2 + 7x = 0.
6 У выражение: с(с – 2)(с + 2) – (с – 1)(с2 + с + 1).
7 Найдите корни уравнения 3x3 – 27x = 0.
8 Разложите на множители многочлен 2х + 2у – х2 – 2ху – у2.
2 вариант.
1°. Вынесите общий множитель за скобки:
а) 2ab – ab2; б) 5a4 – 10a3 + 10a2
2°. Разложите на множители:
а) ax – ay + 2x – 2y; б) 9a2 – 16b2.
3°. Сократите дробь (2a+4)/(a^(2 )- 4).
4°. У выражение (x – 1) (x + 1) – x(x – 3).
5°. Решите уравнение x2 – 25 = 0.
6 У выражение: (х + 1)(х2 + х + 1)
Объяснение:
1. 
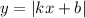- сначала строишь прямую y=kx+b, она проходит через точку (0;b). Затем всю часть графика, которая лежит ниже оси ОХ, отображаешь симметрично относительно этой оси (получится "галка"). Пример: была точка, образно говоря (-3;-5), стала точка (-3;5).
2. 
.
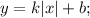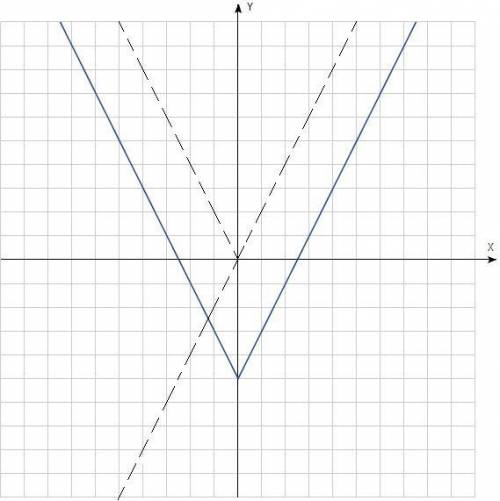
Тут проще так сделать: построить y=kx, затем опять симметрично отобразить всю часть графика относительно оси ОХ (снова получится "галка"), а затем всё это поднять на b единиц (условно поднять, если b<0, то опустить на столько единиц). Получится "висящая" "галка".
3. 
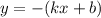
Построй прямую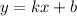 
, а затем у всех точек в координате у поменяй знак. Примеры: было (1;1) стало (1;-1). Было (3;-2), стало (3;2)
4. Если я правильно понял,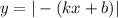 
У модуля есть замечательное свойство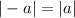 
, поэтому график 4 превращается в график 1.
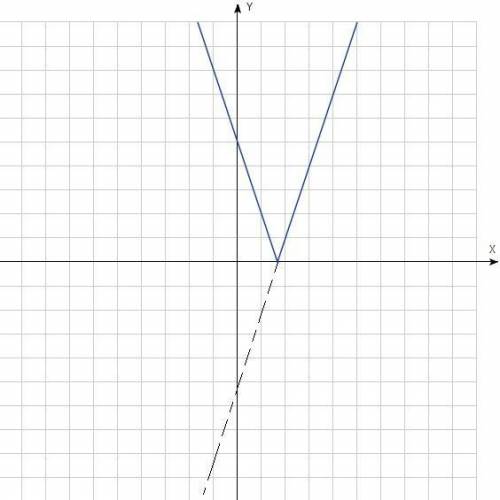
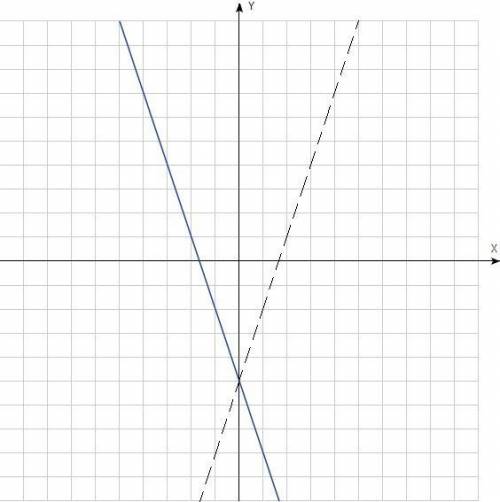
На рисунках пунктирные линии - промежуточные линии, по которым можно ориентироваться и по ним график и строится, путем переносов, отображений и т.д., синия линия - сам график (они по порядку расположены, 1(4), 2,3, т.к. 1=4, судя по условию)
240/2=120
120/2=60
60/2=30
30/2=15
15/3=5
5/5=1
240=2*2*2*2*3*5