ответ: 30°
Объяснение:
1. Проведём из точки S высоту пирамиды SO. Точка O -- это центр ΔABC, лежит на пересечении медиан (так как ABCS -- правильная)
2. SB -- наклонная, SO ⊥ (ABC) ⇒ BO -- проекция SB на (ABC)
3. Так как BO -- проекция SB на (ABC), ∠(SB, (ABC)) = ∠(SB, BO) = ∠SBO -- искомый (по определению угла между прямой и плоскостью)
4. Рассмотрим ΔABC.
BB₁ -- медиана ⇒ СB₁ = 1/2 AC = 9/2
Так как ΔABC -- равносторонний, то
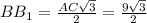
(можно найти и по теореме Пифагора из ΔBB₁C, т.к. BB₁ - высота)
Медианы треугольника пересекаются в одной точке, которая делит их в отношении 2 : 1, считая от вершины. Тогда
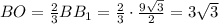
5. Рассмотрим ΔBSO:
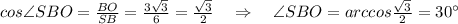

-1 и -4
Объяснение:
x²+5x+4=0 - квадратное уравнение.
ax²+bx+c=0 - общий вид квадратного уравнения.
В нашем случае, а=1, b=5, c=4
Нам надо найти корни этого уравнения.
Корни ищем по схеме:
1) Вычисляем дискриминант по формуле D=b²-4ac
D= 5²- 4*1*4 = 25 - 16 = 9
2) Находим корни по формуле:
x₁ = (-b+√D)/2a
x₂ = (-b-√D)/2a
x₁ = (-5+√9)/2*1 = (-5+3)/2 = -2/2 = -1
x₂ = (-5-√9)/2*1 = (-5-3)/2 = -8/2 = -4
Итак, корни уравнения найдены. Это числа -1 и -4.
Если вы уже проходили эту тему, то корни можно найти и по теореме Виета, т.к. наше уравнение является приведённым, т.к. квадратным уравнением, у которого а=1. Тогда корни можно найти из соотношений
x₁*x₂=c и x₁+x₂= -b
В нашем случае, x₁*x₂=4 и x₁+x₂= -5
Подбором легко найти корни -4 и -1 (их произведение равно 4, а сумма равна -5)
ответ: 30 см
Объяснение:
Якщо суми протилежних сторін чотирикутника рівні, то в такий чотирикутник можна вписати коло. Тому сума бічних сторін трапеції дорівнює сумі основ. В свою чергу середня лінія трапеції дорівнює півсумі основ. Тому сума основ, як і сума бічних сторін трапеції, вдвічі більша за довжину середньої лінії. Тож сума бічних сторін дорівнює 60 см. Так як трапеція рівнобічна, то бічні сторони рівні між собою. Отже довжина бічної сторони дорівнює 60см : 2 = 30см.