120 =32+48+ 40
Объяснение:
Надо представить число 120 в виде суммы трех слагаемых, так что два из них были в отношении 2: 3 , так чтобы произведение было наибольшим.
Пусть первое слагаемое 2х ( 2x>0; x>0), второе слагаемое будет 3х, а третье слагаемое (120 -5х) ( 120-5x>0,то есть x<24) . Тогда рассмотрим функцию произведения данных чисел
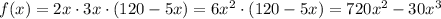
Так как функция непрерывна в точках х=0 и х=24, то найдем наибольшее значение полученной функции на отрезке [0; 24]
Для этого найдем производную данной функции
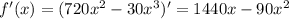
Найдем критические точки, решив уравнение
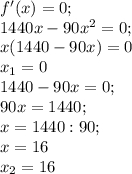
Полученные критические точки принадлежат заданному отрезку. Поэтому найдем значение функции на концах отрезка и в точке х=16
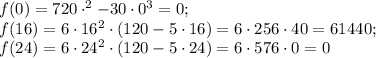
Наибольшее значение функции достигается при х=16. Тогда найдем все слагаемые
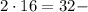 первое слагаемое
первое слагаемое
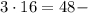 второе слагаемое
второе слагаемое
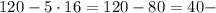 третье слагаемое.
третье слагаемое.
Тогда
120 =32+48+ 40
#SPJ1
а)2sin²x-3sinx-2=0
Замена sinx=t
2t²-3t-2=0
D=3²+4×2×2=25
t₁= 3+√D÷4=3+5÷ 4=8÷4=2
t₂=3-√D÷4=3-5÷4=-2÷4=-0,5
Возвращаемся к замене
sinx=2 sinx=-0,5
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z
4cos²x+4sinx-1=0
cos²x=1-sin²x
4( 1-sin²x)+4sinx-1=0
4-4sin²x+4sinx-1=0
-4sin²x+4sinx-1+4=0
-4 sin²x+4sinx+3=0 ÷(-1)
4sin²x-4sinx-3=0
Замена sinx=t
4t²-4t-3=0
D=4²+4×4×3=16+48=64
t₁=4+√D÷8= 4+8÷8=12÷8=1,5
t₂=4-√D÷8=4-8÷8= -4÷8=-0,5
Возвращаемся к замене
sinx=1,5 sinx=-1\2
решения нет х=(1)⁻k(cтепень)arcsin(-1\2)+πn,n∈Z
-1≤sinx ≥1 x=(1)⁻k × -π\6 +πn,n∈Z