№1
Дана функция
у=6х+19
а) у=? х=0,5 y=6*0.5+19=3+19=22
б) х=?у=1 6x+19=1 6x=-18 x=-3
в) А(-2;7) 6*(-2)+19=-12+19=7 проходит
№2
Построить график функции(только ответы, сам график не нужен)
у=2х-4
б) у=? х=1,5 y=2*1.5-4=3-4=-1
№4
Найти координаты точек пересечения графиков функций
у=47х-37
у=13х+23
47х-37=13х+23 34x=60 x=60/34=30/17 y=13*30/17+23=390/17+23=
№5
Задать формулой линейную функцию, график которой параллелен прямой у=3х-7 и проходит через наяало координат
параллельно прямой значит к=3
проходит через начало координат y=3x
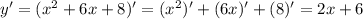
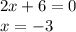
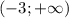, а убывает -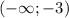 
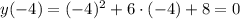
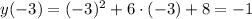- наименьшее
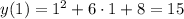- наибольшее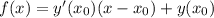
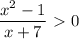
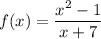
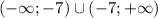
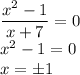
100:(30•3+10)+((90+5•2):(-10)•2=3
1) 100:(30•3+10) = 100:90+10= 100:100=1;
2)((90+5•2):(-10))•2=100:(-10)•2= 100:100•2=2;
3)1+2=3;
Надеюсь все понятно и правильно