ЗАДАЧА:
Расстояние от точки А до точки В= 62 км. На расстоянии 30 км от точки А находится точка С. Из точки А в точку С выехал велосипедист со скоростью 12км/ч, а через 30 минут из точки В в точку С выехал мотоциклист.
ВОПРОС 1: с какой скоростью должен ехать мотоциклист, чтобы встретиться с велосипедистом в точке С?
ВОПРОС 2:
С какой скоростью должен ехать мотоциклист, чтобы приехать в точку С раньше велосипедиста на 1 час 10 минут?
Объяснение:
если от точки А до точки С 30км, то от точки
С до В=62–30=32км. Поэтому велосипедисту до точки С нужно проехать 30км, а мотоциклисту из точки В до точки С - 32 км
Велосипедист со скоростью 12км/ч проедет расстояние 30км за: 30÷12=5/2=2,5 часа
1 ч 10 мин=1 целая 1/6часа или 7/6часа.
Чтобы мотоциклист доехал до точки С раньше велосипедиста на 7/6часа, тогда:
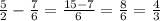
Итак: мотоциклисту нужно добраться до точки С за 4/3 часа. Для этого ему понадобится:
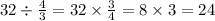
ОТВЕТ 2: мотоциклисту нужно ехать со скоростью 24км/ч, чтобы приехать раньше велосипедиста на 1 час 10 минут.
РЕШЕНИЕ Вопроса 1
30минут=1/2=0,5 часа
Так как мотоциклист выехал через 30 минут после
велосипедиста, то велосипедист за 30 минут проехал: 12÷2=6км и ему осталось проехать 30–6=24км и ему понадобится на это:
2,5 –0,5=2часа.
Соответственно мотоциклисту до встречи с велосипедистом в точке С понадобится также 2часа.
Мотоциклисту нужно за 2 часа проехать 32 км, поэтому ему нужно ехать со скоростью: 32÷2=16км/ч
ОТВЕТ 1: чтобы встретиться с велосипедистом в точке С мотоциклисту нужно ехать со скоростью 16км/ч
Объяснение:
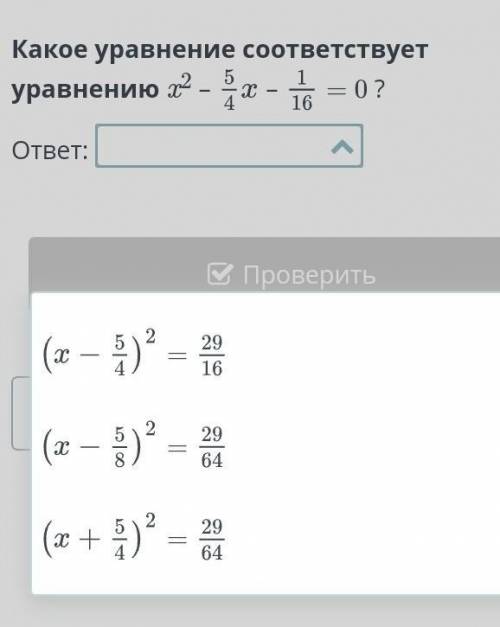
x²- 5/4х-1/16=0
1)(x-5/4)²-29/16=0
x²- 2*5/4х+25/16 -29/16=0
x²- 5/2 х-4/16=0
x²- 5/2 х-1/4=0 НЕТ
1)(x-5/8)²-29/64=0
x²- 2*х*5/8+25/64 -29/16=0
x²- х*5/4 -4/64=0
x²- х*5/4 -1/16=0 ДА
3) (x+5/4)²-29/64=0
x² + х*5/2+25/16 -29/64=0
(уже на этом этапе можно не продолжать вычисления,так,как второй член не соответствует заданному уравнению)