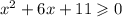
Основное правило: все неравенства, в которых присутствует множитель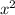 
решаются только методом интервалов. Также только методом интервалов решаются дробные неравенства, если неизвестный множитель стоит в знаменателе.
1) Определим ОДЗ (область допустимых значений):
(
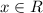— любое число).
2) Приравняем неравенство к нулю и находим корни уравнения:
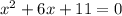
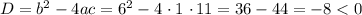
Если дискриминант меньше нуля, то парабола, которая исходит из данного уравнения не имеет общих точек с осью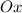 
и, благодаря тому, что 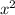положительный, то парабола будет находиться в положительных координатах оси ординат (ось 
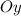). В таком случае, при любом значении икса неравенство будет иметь смысл (потому что в нашем неравенстве стоит знак 
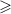, что правильно со значением уравнения. Если бы в таком неравенстве стоял бы знак 
или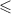 
, то такое неравенство не имело бы смысла, так как сама парабола находиться в положительных значениях оси ординат).
ответ: 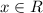( — любое число).
Объяснение:
ответ: при k=-1.