Объяснение:
1.
C⁵ₓ₊₁=(3/8)*A³ₓ
(x+1)!/((x+1-5)!*5!)=(3/8)*x!/(x-3)!
(x+1)!/((x-4)!*5!)=(3/8)*x!/((x-4)!(x-3))
x!*(x+1)/5!=(3/8)*x!/(x-3)
(x+1)/5!=(3/8)/(x-3)
(x-3)*(x+1)=(3/8)*120
x²-2x-3=45
x₂-2x-48=0 D=196 √D=14
x₁=-6 ∉ x₂=8.
ответ: х=8.
2.
Cˣ⁻⁴ₓ₊₁=(7/15)*A³ₓ₊₁
(x+1)!/((x+1-(x-4))!*(x-4)!=(7/15)*(x+1)!/(x+1-3)!
(x+1)!/(5!*(x-4)!=(7/15)*(x+1)!/(x-2)!
1/(5!*(x-4)!)=(7/15)/((x-4)!*(x-3)*(x-2))
1/5!=(7/15)/((x-3)*(x-2))
15*(x-3)*(x-2)=7*5!
15*(x²-5x+6)=7*120 |÷15
x²-5x+6=7*8
x²-5x+6=56
x²-5x-50=0 D=225 √D=15
x₁=-5 ∉ x₂=10.
ответ: х=10.
ответ:: S6 = 10,2
Объяснение:
1. Для определения суммы шести членов арифметической прогрессии необходимо узнать значение шестого ее члена и только тогда найти S6 по формуле
Sn = (a1 + an) : 2 * n.
2. Известна формула для энного члена арифметической прогрессии
аn = a1 + d *(n - 1).
3. Пользуясь этой формулой вычислим разность прогрессии d.
a4 = a1 + d * 3;
1,8 = 1,2 + 3 d;
d = (1,8 - 1,2) : 3 = 0,6 : 3 = 0,2.
4. Теперь найдем а6.
а6 = а1 + d * 5 = 1,2 + 0,2 * 5 = 1,2 + 1 = 2,2.
5. Отвечаем на во задачи
S6 = (a1 + a6) : 2 * 6 = (1,2 + 2,2) : 2 * 6 = 10,2.
x=36
Объяснение:
x=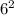
x=36