1.
а) 3(a + 2) + b(a + 2) = (3 + b) * (a + 2)
б) 4f(5m-3n) - 5r(5m-3n) = (4f - 5r) * (5m - 3n)
в) 5m(a - 3d) + a - 3d = 5m(a - 3d) + 1(a - 3d) = (5m + 1) * (a - 3d)
г) 5m(a - 3d) - a + 3d = 5m(a - 3d) + 1(a - 3d) = (5m + 1) * (a - 3d)
2.
а) 3a +6 + ab + 2b = 3(a + 2) + b(a + 2) = (3 + b) * (a + 2)
б) 20fr - 12fn - 25rm + 15mn = 4f(5r - 3n) - 5m(5r -3n) = (4f - 5m) * (5r - 3n)
в) ab + ac + af + b + c + f = a(b + c + f) + 1(b + c + f) = (a + 1) * (b + c + f) (думаю, у Вас тут ошибка, и должна быть именно буква b)
г) x⁵ + x⁴ + x³ +x² + x + 1 = x⁵ + x⁴ + x³ +x² + x¹ + 1 = x³(x² + x¹ + 1) + 1(x² + x¹ + 1) = (x³ + 1) * (x² + x¹ + 1)
Это просто
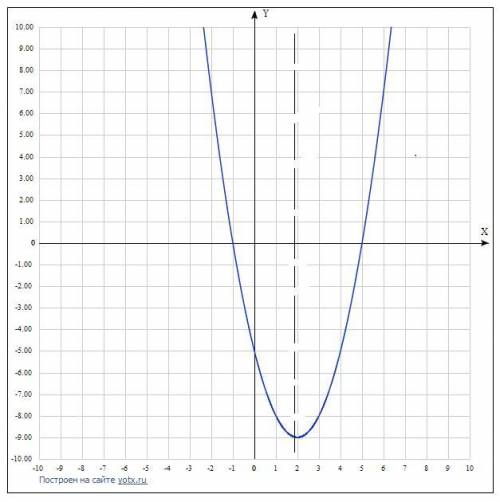
так как есть х²- это график параболы, при х² нет минуса, значит ветви параболы направлены вверх. Теперь надо найти точку пересечения параболы с осью ОУ .для этого х=0
у=0²-4*0-5=-5 . Точка пресечения с осью ОУ (0;-5)
Теперь найдём точки пересечения с осью ОХ (у=0)
х²-4х-5=0
D= 4²-4*1*(-5)=16+20=36

первая точка пересечения с осью ОХ (-1;0), вторая (5;0)
Посередине между этими точками будет ось симметрии параболы ( отметим штрихом на графике)
ну ещё пар точек определим при х=2
у= 2²-4*2-5= -9 точка(2;-9)- вершина параболы
Составим таблицу точек:
х | y
-2 | 7
-1 | 0
0 | 5
1 | -8
2 | -9
3 | -8
4 | -5
5 | 0
6 | 7
ответ:Надо решить неравенство - 3x^2 + 4x - 1 > 0. Решим методом интервалов.
1. Найдем нули функции.
- 3x^2 + 4x - 1 = 0;
D = b^2 - 4ac;
D = 4^2 - 4 * (- 3) * (- 1) = 16 - 12 = 4; √D = 2;
x = (- b ± √D)/(2a);
x1 = (- 4 + 2)/(2 * (- 3)) = - 2/(- 6) = 1/3;
x2 = (- 4 - 2)/(- 6) = - 6/(- 6) = 1.
2. Отметим числа 1/3 и 1 на числовой прямой. Эти числа делят числовую прямую на три интервала: 1) (- ∞; 1/3), 2) (1/3; 1), 3) (1; + ∞).
3. Проверим знак выражения (- 3x^2 + 4x - 1) на каждом интервале. На 1 и 3 интервалах это выражение принимает отрицательные значения, а на 2 интервале - положительные. Значит, второй интервал является решением нашего неравенства.
ответ. (1/3; 1).
Объяснение: