Объяснение:
эти уравнения решаются совсем не сложно,особенно если можешь приводить дроби к общему знаменателю и решать простые уравнения.
Т.к в знаменателе этих уравнений стоят натуральные числа,то мы можем "избавиться "от этих знаменателей,для этого надо найти их общий знаменатель и после умножения сократить.
решение двух примеров внизу.все остальные решаются аналогично.попробуй решить самостоятельно,смотри на мое решение.вся сложность заключается в нахождении общего знаменателя.,для этого надо найти НОК старых знаменателей.
Перечислим соображения, необходимые для решения задачи:
1) В первом случае пешеход преодолеет расстояние в 3/8 моста;
во втором - 5/8 моста.
2) В каком бы направлении он ни побежал, скорость его бега одинакова - х км/ч.
3) В первом случае до встречи пешехода с машиной бы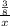 
часов (далее обозначим эту величину 
);
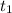во втором -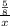 
часов (далее - 
).
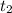4) Составим отношение времени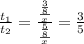 
.
5) Обозначим расстояние между автомобилем и пешеходом буквой S.
В обоих случаях расстояние S сокращалось до нуля, т.е. автомобиль и пешеход сближались относительно друг друга.
6) В первом случае скорость этого сближения равна (60+x)км/ч,
во втором - (60-x)км/ч.
7) Тогда время 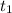можно выразить, как 
;
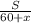время 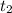можно выразить, как 
.
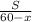8) Мы уже знаем, что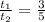 
, значит
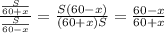
Далее,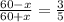 
, откуда x=15.
4^x -18*2^x+32=0
2^(2x) - 18*2^x+32=0
t=2^x
t^2-18t+32=0
t1+t2=18
t1t2=32
t=16;t=2
2^x=16; 2^x=2
x=4; x=1
ответ: 4;1