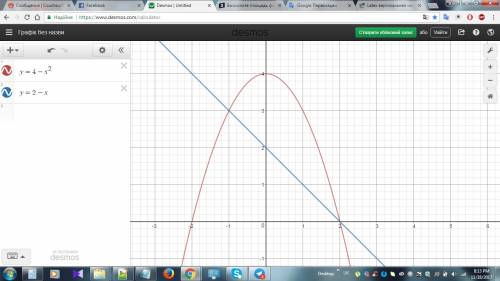
Теперь посмотрим где расположена фигура. Нам важно, какой график выше (относительно другого графика), а какой – ниже.
Из графика видно, что выше расположена парабола y=4-x² , а ниже прямая y=2-x.
Формула для вычисления площади: 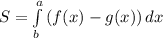 где
где  это функция которая расположена выше, чем функция
это функция которая расположена выше, чем функция 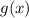
таким образом для исчисления площади нужно взять интеграл
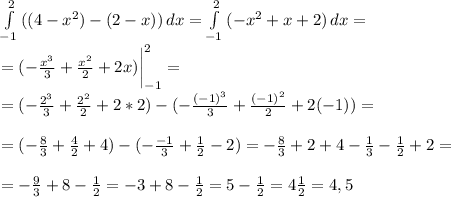
zₓ'=((x+2y)*y²)ₓ'=(xy²+2y³)ₓ'=(xy²)ₓ'+(2y³)ₓ'=y²+0=y²
Частная производная по у (при переписывании вместо а надо писать у, в предложенных индексах нет такой буквы, потому использую а:
zₐ'=((x+2y)*y²)ₐ'=(xy²+2y³)ₐ'=(xy²)ₐ'+(2y³)ₐ'=2xy+6y²
в) zₓ'=(9(x-y²)⁴)ₓ'=9*((x-y²)⁴)ₓ'*(x-y²)ₓ'=9*4*(x-y²)³*1=36(x-y²)³
zₐ'=((9(x-y²)⁴)ₐ'=9*((x-y²)⁴)ₐ'*(x-y²)ₐ'=9*4*(x-y²)³*(-2y)=-72y(x-y²)³
б) zₓ'=(cos(2x+e^y))ₓ'=(cos(2x+e^y))ₓ'*(2x+e^y)ₓ'=-sin(2x+e^y)*2=-2sin(2x+e^y)
zₐ'=(cos(2x+e^y))ₐ'=(cos(2x+e^y)ₐ'*(2x+e^y)ₐ'=-sin(2x+e^y)*e^y