y = x³ + 3x² - 45x - 2
Найдём производную :
y' = (x³)' + 3(x²)' - 45(x)' - 2' = 3x² + 6x - 45
Приравняем производную к нулю и найдём критические точки :
3x² + 6x - 45 = 0
x² + 2x - 15 = 0
По теореме Виета :
x₁ = - 5
x₂ = 3
Найдём значения функции в критических точках и на концах отрезка и сравним их .
y(- 5) = (- 5)³ + 3 * (- 5)² - 45 * (- 5) - 2 = - 125 + 75 + 225 - 2 = 173
y(3) = 3³ + 3 * 3² - 45 * 3 - 2 = 27 + 27 - 135 - 2 = - 83
y(- 8) = (- 8)³ + 3 * (- 8)² - 45 * (- 8) - 2 = - 512 + 192 + 360 - 2 = 38
y(8) = 8³ + 3 * 8² - 45 * 8 - 2 = 512 + 192 - 360 - 2 = 342
y(наим) = - 83
y(наиб) = 342
 и
и  то для площади и периметра получатся выражения:
то для площади и периметра получатся выражения: ;
;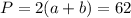 ;
;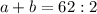 ;
;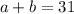 ;
; ;
;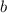 в формулу для площади:
в формулу для площади: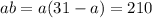 ;
; ;
;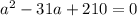 ;
; ;
; ;
;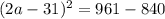 ;
;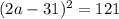 ;
;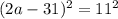 ;
;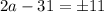 ;
;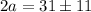 ;
; ;
; м ;
м ;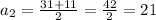 м ;
м ; в формулу для
в формулу для 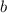 :
: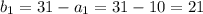 м ;
м ; м ;
м ;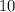 метров и
метров и 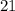 метр.
метр.
1) 3(25 + x) = 9(25 - x)/2
75+3x= (225-9x)/2 /*2
150+6x=225-9x
15x=225-150
15x=75
x=5 км/ч - скорость течения реки
2) Пусть 1-ый выполнит работу за х часов, тогда 2-ой за х+12 часов, всю работу примем за 1, тогда имеем уравнение:
1/х + 1/х+12 = 1/8, приводим левую часть к общему знаменателю, получим:
(2х+12)/(х^2+12х) = 1/8
х^2 + 12х = 16х + 96
x^2 - 4х - 96 = 0, решаем квадратное ур-е:
D = b^2 - 4ac = 16 + 384 = 400
х = - b + корень квадратный из 400/2a
х = (4+20)/2 = 12 часов - выполнит работу 1-ый
12+12=24 часа = выполнит работу 2-ой