Рассмотрим первое уравнение:
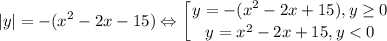
Данную совокупность можно представить в виде графика: начертим две параболы и оставим только их части выше (в первом случае) и ниже (во втором) оси абсцисс.
Рассмотрим второе уравнение:
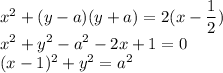
Оно задаёт окружность радиусом |a|.
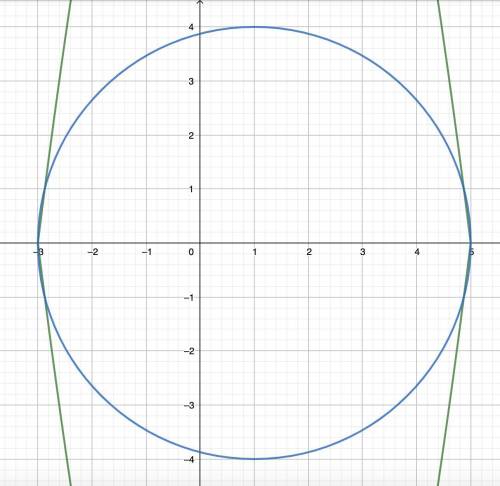
Оба графика симметричны относительно прямых y = 0 и x = 1. Если окружность касается парабол внутренним образом, система имеет 4 решения, затем, если увеличивать радиус, при пересечении она имеет 8 решений. Когда окружность проходит через общие точки частей парабол (-3; 0), (5; 0), система имеет 6 решений. Затем при пересечении — 4 решения, при внешнем касании — 2 решения.
В случае, когда реализуется 6 решений, окружность проходит через точку (5; 0). Её центр расположен в точке (1; 0). Значит, радиус равен 4:
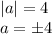
ответ: ±4
В решении.
Объяснение:
2) Пусть аn есть арифметическая прогрессия. Если а1=-10 и а3=-4, с характеристического свойства найдите а2. Определите значение девятого члена прогрессии.
а) а₁ = -10;
а₃ = -4;
а₂ = ?
а₂ = (а₁ + а₃)/2
а₂ = (-10 - 4)/2
а₂ = -14/2
а₂ = -7;
б) a₉ = ?
an = a₁ + d(n - 1);
а₉ = а₁ + d(n - 1);
Найти d:
d = a₂ - a₁;
d = -7 - (-10)
d = -7 + 10
d = 3;
а₉ = а₁ + d(n - 1);
а₉ = (-10) + 3(9 - 1)
а₉ = (-10) + 24
а₉ = 14.
3) в арифметической прогрессии (аn) известно, что d=2,a1=5. Найти s13.
а₁ = 5;
d = 2;
S₁₃ = ?
Формула:
Sn = ((2a₁ + d(n - 1))/2 * n
S₁₃ = (2 * 5 + 2 * 12)/2 * 13
S₁₃ = (10 + 24)/2 * 13
S₁₃ = 17 * 13
S₁₃ = 221.