1. 1) Очевидно
2) Очевидно
3) Очевидно ибо под учеником подразумевается 12 девочек и 13 мальчиков, т.е. всего учеников 12 + 13 = 25.
4) К любой из 12 девочек в пару можно взять любого из 13 мальчиков. По правилу произведения всего существует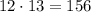 
выбрать мальчика с девочкой.
ОТВЕТ: 1) 12; 2) 13; 3) 25; 4) 156.
2. Есть 10 цифр, из которых нужно составить четырехзначные числа.
1) Если цифры не могут повторяться, рассуждаем следующим образом. На первом месте может стоять любая из цифр, кроме 0, т.е. существует выбрать цифру, обозначающую тысячи. На втором месте может стоять любая из 9 оставшихся цифр, т.е. цифру, обозначающую сотни, также можно выбрать Аналогично цифру, обозначающую десятки, можно выбрать так как останется 8 цифр; цифру, обозначающую единицы
По правилу произведения всего можно составить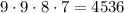 
четырехзначных чисел.
2) Если цифры не могут повторяться, рассуждаем следующим образом. На первом месте может стоять любая из цифр, кроме 0 - имеем выбора первой цифры. Однако так как цифры могут повторяться, каждую следующую цифру числа можно выбрать
По правилу произведения всего можно составить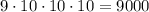 
четырехзначных чисел.
ОТВЕТ: 1) 4536; 2)9000.
1)Решение системы уравнений х₁= -5 х₂=8
у₁= -3,375 у₂=5,4
2)Решение системы уравнений х=9/40
у=1/40
Объяснение:
1)1/(2х-3у)+х=3
х/(2х-3у)= -40
Умножаем оба уравнения на (2х-3у), чтобы избавиться от дроби:
1+х(2х-3у)=3(2х-3у)
х= -40(2х-3у)
Раскрываем скобки:
1+2х²-3ху=6х-9у
х= -80х+120у
Во втором уравнении выразим у через х:
-120у= -80-х
-120у= -81х
у= -81х/-120 сократим дробь на 3:
у=27х/40
Подставим значение у в первое уравнение:
1+2х²-3ху=6х-9у
1+2х²-3х*(27х/40)=6х-9*(27х/40)
1+2х²-81х²/40=6х-243х/40
Умножим уравнение на 40, чтобы избавится от дроби:
40*1+40*2х²-81х²=40*6х-243х
Выполним умножение и перенесём оставшиеся неизвестные в левую часть уравнения:
40+80х²-81х²-240х+243х=0
Приведём подобные члены:
-х²+3х+40=0
х²-3х-40=0, квадратное уравнение, ищем корни:
х₁,₂=(3±√9+160)/2
х₁,₂=(3±√169)/2
х₁,₂=(3±13)/2
х₁= -10/2
х₁= -5
х₂=16/2
х₂=8
Вычислим у:
у=27х/40
у₁=27*(-5)/40
у₁= -135/40
у₁= -3,375
у₂=27*8/40 сокращение на 8
у₂=27/5
у₂=5,4
Решение системы уравнений х₁= -5 х₂=8
у₁= -3,375 у₂=5,4
2)1/(х+у)+1/(х-у)=9
7/(х+у)+9/(х-у)=73
Общий знаменатель (х-у)(х+у), надписываем над дробями дополнительные множители, избавляемся от дроби:
(х-у)+(х+у)=9(х-у)(х+у)
7(х-у)+9(х+у)=73(х-у)(х+у)
Умножим первое уравнение на -7, сложим уравнения по методу алгебраического сложения и выразим х через у.
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, чтобы коэффициенты при неизвестном каком-то были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают уравнения, можно умножать обе части уравнения на одно и то же число, делить.
-7(х-у)-7(х+у)= -63(х-у)(х+у)
7(х-у)+9(х+у)=73(х-у)(х+у)
Складываем уравнения:
-7(х-у)+7(х-у)-7(х+у)+9(х+у)=-63(х-у)(х+у)+73(х-у)(х+у)
Приводим подобные члены:
2(х+у)=10(х-у)(х+у) сократим на 2(х+у):
1=5(х-у)
1=5х-5у
-5х= -5у-1
5х=5у+1
х=5у+1/5
Получили выражение х через у. Подставим выражение в первое уравнение и вычислим у:
(х-у)+(х+у)=9(х-у)(х+у)
х-у+х+у=9(х-у)(х+у)
2х=9(х-у)(х+у), или по формуле разности квадратов:
2х=9(х²-у²)
2х=9х²-9у²
2*(5у+1/5)=9(5у+1/5)²-9у²
[2(5у+1)]/5=[9(25у²+10y+1)]/25-9у²
(10у+2)/5=(225у²+90у+9)/25-9у²
Умножим уравнение на 25, чтобы избавиться от дроби:
5(10у+2)=225у²+90у+9-25*9у²
Перенесём неизвестные в левую часть, известные в правую)
50у-225у²-90у+225у²=9-10
Приводим подобные члены:
-40у= -1
у= -1/-40
у=1/40
Вычисляем х:
х=5у+1/5
х=(5*1/40)/5
х=(9/8)/5=9/40
х=9/40
Решение системы уравнений х=9/40
у=1/40
Если это система, где нужно найти пересечение, то вот решение: