постройте график функции у = 2х - 4.Найдите точки пересечения графика осями координат СОР

👇

Увидеть ответ

Ответ:

Аняняняняняняняяня

24.09.2020

у=2х - 4 ( прямая)

Пересечение с осью ОХ ⇒ у=0

2х-4=0

2х=4

х = 4/2

х=2

Координаты точки пересечения с осью абсцисс ОХ: В(2;0)

Пересечение с осью ОУ ⇒ х=0

у=2*0- 4

у= - 4

Координаты точки пересечения с осью ординат ОУ : С(0;-4)

График в приложении.

А(-2,7) ⇒ 7 ≠ 2*(-2) - 4 ; 7 ≠ - 8

Точка А(-2,7) не принадлежит графику функции у=2х-4

4,6(45 оценок)

Открыть все ответы

Ответ:

Lolkek3332

24.09.2020

1) Не совсем понятно cosx умножается на всю дробь или только на икс.
В первом случае будет ноль, т.к. синус и косинус функции периодические, их произведение изменяется не более, чем от плюс до минус единицы. А Всё делится на бесконечность. Второй случай сложнее, периодически встречаются бесконечные разрывы, тогда предел будет плюс или минус бесконечность.

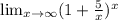
2) $\lim_{x \to \infty} (1+ \frac{5}{x} ) ^{x}$
Сделаем замену t=5/x, тогда t→0 и x=5/t
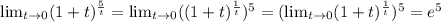
$\lim_{t \to \inft0} (1+t) ^{ \frac{5}{t} } = \lim_{t \to \inft0} ((1+t) ^{ \frac{1}{t}}) ^{5} =( \lim_{t \to \inft0} (1+t) ^{ \frac{1}{t} } ) ^{5} = e^{5}$
Использован второй замечательный предел: $\lim_{t \to \inft0} (1+t) ^{ \frac{1}{t} } =e$

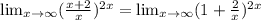
3) $\lim_{x \to \infty} ( \frac{x+2}{x}) ^{2x} =\lim_{x \to \infty} (1+ \frac{2}{x} ) ^{2x}$
Сделаем замену t=2/x, тогда t→0 и x=2/t
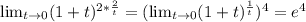
$\lim_{t \to \inft0} (1+t) ^{ 2*\frac{2}{t} } =(\lim_{t \to \inft0} (1+t) ^{ \frac{1}{t} } ) ^{4} = e^{4}$

4) $\lim_{x \to \infty} (1+ \frac{2}{3x} ) ^{3x}$
Сделаем замену t=2/(3x), тогда t→0 и x=2/(3t)
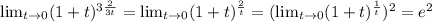
$\lim_{t \to \inft0} (1+ t} ) ^{3 \frac{2}{3t}} =\lim_{t \to \inft0} (1+ t} ) ^{ \frac{2}{t}}=(\lim_{t \to \inft0} (1+ t} ) ^{ \frac{1}{t}}) ^{2} = e^{2}$

Т.о. везде делаются преобразования, чтобы использовать второй замечательный предел.

4,4(99 оценок)

Ответ:

ЛаураАлинина

24.09.2020

а и а^2 здесь можно представить в виде любого числа. Попробуем это сделать. Для начала, выясним, при каких значениях а=а^2. Естественно, условие выполняется при значении 0, также ему удовлетворяют значения 1 и -1. Возаедём их для ясности в квадрат и получим:

1×1=1

-1×(-1)=1. Следовательно, 1=1 и а =а^2.

Теперь выясним, почему же при других значениях а<а^2. Подставим нппример значение 2. Тогда получим, что 2^2=4 и 2<4. А если вдруг число будет отрицательным? Попробуем подставить и получим:

-2^2=-2×(-2)=4. Соответственно, получим такое неравенство:

2<-4. Проведя такое доказательство, можно прийти к выводу, что а<=а^2.

4,4(82 оценок)

Это интересно:

Компьютеры-и-электроника

17.05.2021

Mac и внешний жесткий диск: как загрузить компьютер...

Кулинария-и-гостеприимство

10.10.2022

Как правильно разбить яйцо: советы и инструкции...

Здоровье

18.03.2020