Question

Arctgx=arcsin(x/sqrt(1+x^2))
нужно доказать люди добрые

Answer 1

Введем замену: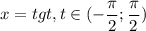 $x=tgt, t\in (-\dfrac{\pi}{2};\dfrac{\pi}{2})$ . Отметим, что область определения исходного выражения - все действительные числа, и при этом множество значений 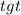$tgt$ на интервале 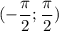$(-\dfrac{\pi}{2};\dfrac{\pi}{2})$, очевидно, также все действительные числа. А значит полученное после замены выражение равносильно исходному

$arctg(tgt)=arcsin\dfrac{tgt}{\sqrt{1+tg^2t}}\\ t=arcsin\dfrac{|cost|tgt}{\sqrt{cos^2t+sin^2t}}\\ t=arcsin\dfrac{cost\cdot tgt}{1}\\ t=arcsin(sin t)\\ t=t$

- верно

Ч.т.д.