1. 23
2. 73,9
3. -7,5
4. -17,4375
Объяснение:
1. а16=а1+(n-1)*d
a16=-7+(16-1)*2
a16=-7+15*2
a16=-7+30=23
2. a11=-11,9+7,8*11=73,9
3. a1=1,9-0,3*1=1,6
a15=1,9-0,3*15=-2,6
S15=a1+a15/2*15=1,6+(-2,6)/2*15=-7,5
4.a₁=-7,2; a₂=-6,9
Сначала найдем разность этой арифметической прогрессии:
d=a₂-a₁=-6,9-(-7,2)=0,3
Выпишем формулу общего члена и подставим туда известные нам значение:
an=а₁+d(n-1)=-7,2+0,3(n-1)
Теперь можем найти число (n) отрицательный членов этой прогрессии, решив неравенство:
-7,2+0,3(n-1)<0
-7,2+0,3n-0,3<0
0,3n<0,75
n=2,5
Sn=2a1+d(n-1)/2*n
S2,5=-14,4+0,45/2*2,5=-17,4375
Решите систему :
{ (1/3x +1/4y+5/12z)(x/3+y/4+5z/12) =1 ;
{ x³+3y²-7z =6
{xy > 0
{xz >0
{yz >0
ответ: (2 ; 2 ;2) ;
((-5-√13)/2;(-5-√13)/2;(-5-√13)/2 ) , ( (-5+√13)/2 ;(-5 +√13)/2 ;(-5+√13)/2).
Объяснение: Область Определения Системы x ≠0 ,y ≠0 , z ≠0
Очевидно( показывают три неравенство системы) , переменные системы x , y и z одного знака .
{ (1/3x +1/4y+5/12z)(x/3+y/4+5z/12) =1 ;
{ x³+3y²-7z =6
* * * (x/y+y/x -2) = (x²-2xy+y²) /xy = (x-y)²/xy ≥0 и т.д * * *
Удачи ! Решение во вложение
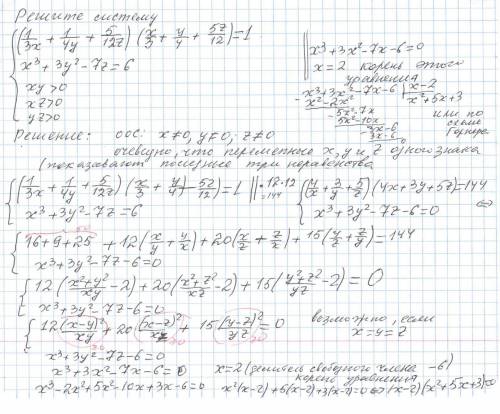
–4
Объяснение:
Стандартный алгоритм нахождения наименьшего значения функции y=f(x) на отрезке [a; b] следующее:
1) находим критические точки функции, которые входят в заданный отрезок [a; b], то есть найдем производную функции f(x) и находим нули производной на отрезке [a; b] (решаем уравнение f '(x)=0);
2) вычислим значения функции f(x) для критических точек из отрезка [a; b] и для граничных значений a и b;
3) ответом будут наименьшее значение среди полученных значений функции.
Дана функция y = (x–9)²·(x+4)–4 и отрезок [7; 16].
1) находим критические точки функции:
y'=((x–9)²·(x+4)–4)'=((x–9)²)'·(x+4)+(x–9)²·(x+4)'–(4)'=
=2·(x–9)²⁻¹·(x+4)+(x–9)²·1–0=2·(x–9)·(x+4)+(x–9)²=
=(x–9)·(2·x+8+x–9)=(x–9)·(3·x–1)
y'=0 ⇔ (x–9)·(3·x–1)=0 ⇔ x=9 ∈ [7; 16], x=1/3 ∉ [7; 16].
2) вычислим значения функции f(x) для критической точки x=9, граничных точек x=7 и x=16:
y(7)= (7–9)²·(7+4)–4 = 4·11–4 = 44–4 = 40
y(9)= (9–9)²·(9+4)–4 = 0·13–4 = –4
y(16)= (16–9)²·(16+4)–4 = 49·20–4 = 980–4 = 976
Среди найденных значений выбираем наименьшее, то есть:
y(9) = –4.