Пусть функция 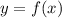 определена на отрезке
определена на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png)
Разобьём отрезок произвольным образом на n частей точками:
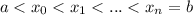
В каждом интервале произвольным образом выбираем точку
![c_{i}\in [x_{i-1};x_{i}]](/tpl/images/1361/6254/a2b9c.png)
Cумма
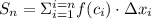 ,
,
где 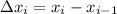 - длина частичного отрезка
- длина частичного отрезка ![[x_{i-1};x_{i}]](/tpl/images/1361/6254/3b10f.png) ,
,
называется интегральной суммой функции 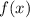 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) .
.
Определенным интегралом от функции 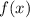 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) называется предел интегральных сумм
называется предел интегральных сумм 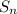 , при условии, что длина наибольшего частичного отрезка стремится к нулю
, при условии, что длина наибольшего частичного отрезка стремится к нулю
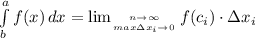
Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции
Пусть функция 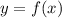 определена на отрезке
определена на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png)
Разобьём отрезок произвольным образом на n частей точками:
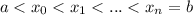
В каждом интервале произвольным образом выбираем точку
![c_{i}\in [x_{i-1};x_{i}]](/tpl/images/1361/6254/a2b9c.png)
Cумма
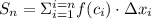 ,
,
где 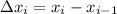 - длина частичного отрезка
- длина частичного отрезка ![[x_{i-1};x_{i}]](/tpl/images/1361/6254/3b10f.png) ,
,
называется интегральной суммой функции 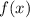 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) .
.
Определенным интегралом от функции 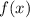 на отрезке
на отрезке ![[a;b]](/tpl/images/1361/6254/a6d4a.png) называется предел интегральных сумм
называется предел интегральных сумм 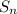 , при условии, что длина наибольшего частичного отрезка стремится к нулю
, при условии, что длина наибольшего частичного отрезка стремится к нулю
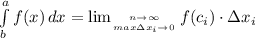
Геометрическая интерпретация определённого интеграла - площадь криволинейной трапеции
Відповідь:
графиком функциии есть парабола , ее ветки направлены вверх
Пояснення:
начерти параболу вершиной которой будут указанные кординаты