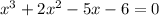Подбором найдем первый корень уравнения. Просто подставляем числа 0, 1, -1, 2, -2 и т.д. и проверяем равенство. Но как правило слишком долго подбирать не приходится. Первый корень х=2
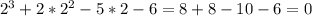. В первой скобке получается (х-2), определим что получается во второй. Чтобы получился х³, нужно скобку
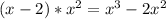, У нас в примере +2х², значит к х² прибавляем 4х получается 
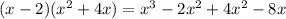. Далее должно остаться -5х, следовательно прибавляем 3 
= 
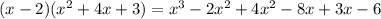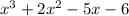
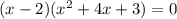
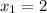и 
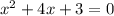
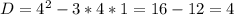
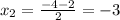
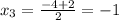
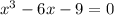Решаем таким же методом, как и предыдущее уравнение. Подбором определяем один из корней, это х=3 проверяем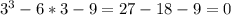 
; 
; 
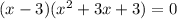
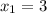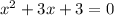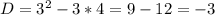D<0 действительных корней нет. Если по заданию надо найти действительные корни, то ответ: х=3 - один корень. Если такого условия нет, то к нему добавятся два комплексных корня и получится ответ: х=3, 
; 
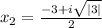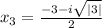
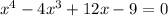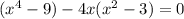
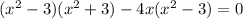
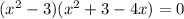
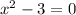
Разложим на множител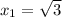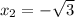и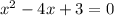
; 
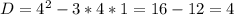
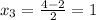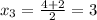
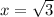и 
; 
; 
и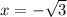 
Решение:
Для простоты решения введем новые переменные
z =xy и t =x-y
Перепишем наши уравнения с новыми переменными
{хy-(x-y)=7
{ху+(х-y)=13
{z-t=7
{z+t=13
Суммируем первое и второе уравнение найдем z
z-t=7
+ z+t=13
2z =20
z=10
Из второго уравнения находим t
t =13-z =13-10 =3
Получили новую систему уравнений
{xy=10
{x-y=3
Из второго уравнения выразим переменную y
и подставим в первое уравнение
y=x-3
x(x-3)=10
x²-3x-10=0
D=3²-4*(-10) = 9 + 40 = 49
x1= (3-7)/2 = -2
x2 = (3+7)/2 = 5
y1 = x-3 = -2-3 = -5
y2 = x-3 = 5-3 = 2
Получили две пары ответов(-2;-5) и (5;2)