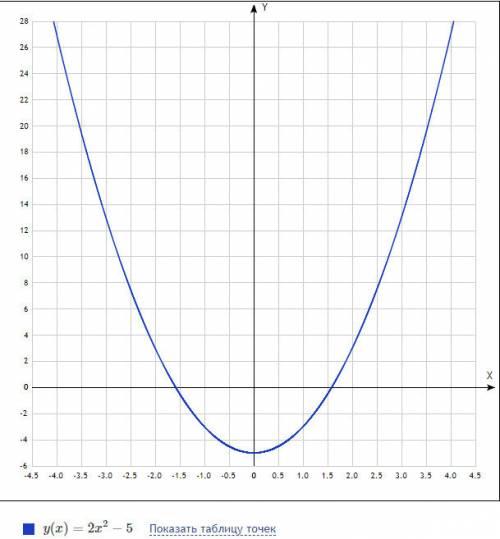
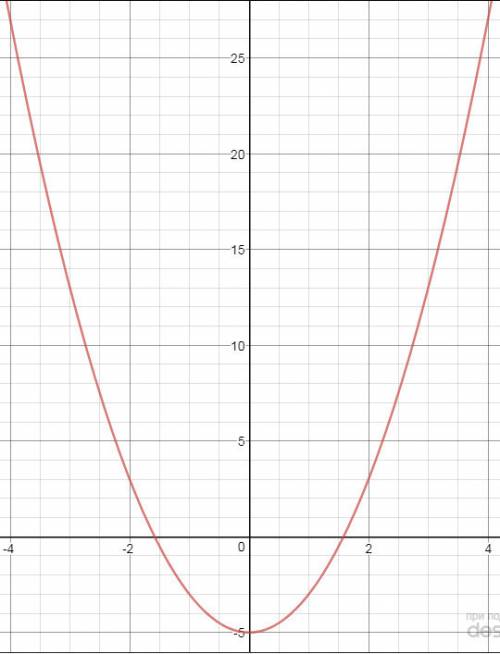
График квадратичной функции - парабола с вершиной в т.А (0; -5), проходящей через т.В (4; 27). Задать эту функцию формулой
Решение.
График квадратичной функция определяется уравнением(формулой)
y = ax² + bx + с
Для решения задания нужно найти значения a, b, c
Вершина параболы определяется координатами
x = -b/(2a) y = a(b/(2a))² + b(-b/(2a)) + c
В нашем случае х = 0.
Поэтому -b/(2a) = 0 ⇒ b = 0
При х = 0 y(0) = c
Следовательно с = -5
Для нахождения значения коэффициента а используем координаты второй точки параболы В (4; 27)
a*4²- 5 = 27
16a = 32
a = 2
Получили уравнение параболы удовлетворяющее заданию
y = 2x² - 5
Пусть x₁и x₂ - нули квадратичной функции y = 4x² - (3a + 2) x + a - 1. Найти, при каких значениях выполняется неравенство x₁ < 3 < x₂.
Решение.
Так как коэффициент перед x² больше 0(4>0), то ветви параболы направлены вверх. Точки x₁ и x₂ определяют нули функции в которых значение функции равно нулю(y(x₁) = y(x₂) = 0).
Исходя из этого можно сделать вывод, что при х = 3 значение функции меньше нуля.
y(3) < 0
y(3) = 4·3² - (3a + 2)·3 + a - 1 = 36 - 9a - 6 + a - 1 = 29 - 8a
29 - 8a < 0
8a > 29
a > 3,625
Поэтому для функции y = 4x² - (3a + 2) x + a - 1 неравенство x₁ < 3 < x₂ истинно для всех значених a∈(3,625;+∞)
ответ: a∈(3,625;+∞)
Оксана обещала выйти замуж за кузнеца Вакулу,если он принесёт ей в подарок черевички (туфли) ,которые носит сама царица. Кузнец выполнил её царица подарила ему туфли для Оксаны. Она согласилась выйти за него замуж не только за подарок,а потому что полюбила его.