
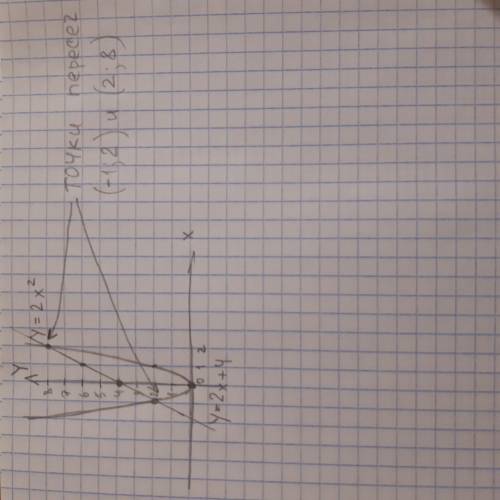
(-1;2) и (2;8)
Объяснение:
1)У=2х² это парабола ветви вверх
Ищем точки :
Х 0 1 2
У 0 2 8
Черти координатную плоскость и отмечай эти точки на ней, затем соединяй и дорисовывай зеркальную часть параболы
Подпиши этот график у=2х²
2)у=2х+4 это прямая, для нее достаточно 2 точки
Х 0 1
У 4 6
На той же плоскости где уже начерчена парабола, отмечай точки и соединяй их, прямую веди так чтоб она пересекла график параболы, ведь прямая бесконечна и ее можно продлить за точки
Затем ищешь точки соприкосновения этих графиков
x - 4*V(x + 4) - 1 < 0 ( V - корень квадратный).
x - 1 < 4*V(x + 4)
Правая часть неравенства <= 0 для всех х из ОДЗ, левая часть < 0 при x < 1, то есть неравенство выполняется при x < 1,
с учетом ОДЗ получаем -4 <= х < 1.
Пусть x >= 1.
Возведем обе части неравенства в квадрат
(x - 1)^2 < 16*(x + 4)
x^2 - 2*x + 1 < 16*x + 64
x^2 - 18*x - 63 < 0
Равенство верно на интервале между корнями уравнения.
Корни х1 = -3, х2 = 21, неравенство выполняется для -3 < х < 21, с учетом x >= 1 получаем 1 <= х < 21.
Объединяем условия -4 <= х < 1 и 1 <= х < 21, получаем
ответ: -4 <= х < 21.