Линейное уравнение
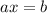
имеет единственное решение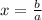 
если a≠0
имеет бесчисленное множество решений, если a=0 и b=0
не имеет решений, если a=0; b≠0
1) ах-3=b ⇒ ax=b+3
единственное решение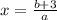 
если a≠0
2)4+bх=а ⇒ bx=a-4
единственное решение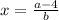 
если b≠0
3)b=а(х-3) ⇒ ax=b+3a
единственное решение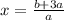 
если a≠0
4)4=а-(bх-1) ⇒ bx=a-3
единственное решение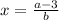 
если b≠0
5) условие написано некорректно.
2х-(а/b)=3 ⇒ 2x=(a/b)+3
единственное решение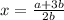 
если b≠0
или
(2х-а)/b=3 ⇒ 2x=3b+a
единственное решение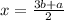 
6)условие написано некорректно.
(1-bх)/а=1 ⇒1-bx=a⇒ bx=1-a
единственное решение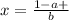 
если b≠0
1-(bх/а)=1⇒ bx/a = 0 ⇒ x=0
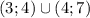
Объяснение:
Решим первое неравенство. ОДЗ:
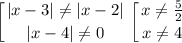
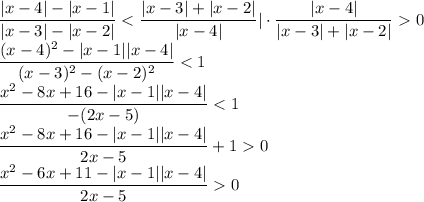
Если x < 1 или x ≥ 4, то модули раскрываются с одним знаком, произведение подмодульных выражений положительно:
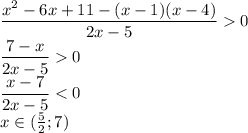
Учитывая, что x < 1 или x ≥ 4, а также учитывая ОДЗ,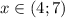 
Если 1 ≤ x < 4, то модули раскрываются с разным знаком, произведение подмодульных выражений отрицательно:
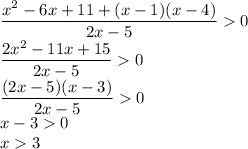
Учитывая, что 1 ≤ x < 4 и ОДЗ,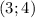 
.
Объединяя полученные промежутки, получаем, что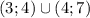
Решим второе неравенство. Пусть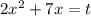 
. Тогда
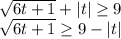
Если правая часть отрицательна, то неравенство выполняется на ОДЗ, так как квадратный корень всегда неотрицателен:
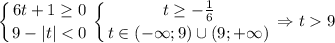
Если правая часть неотрицательна, то обе части можно возвести в квадрат:
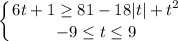
Если t ≥ 0, то модуль раскрывается с плюсом, первое неравенство имеет вид:
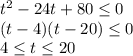
Если t < 0, то модуль раскрывается с минусом, неравенство имеет вид:
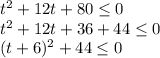
Сумма неотрицательного и положительного чисел не может быть неположительной. В данном случае решений нет.
Учитывая -9 ≤ t ≤ 9, решением данного случая является ![t\in[4;9]](/tpl/images/1358/7181/70120.png)
Объединив оба случая, получаем t ≥ 4,
![2x^2+7x-4\geq 0\\(x+4)(2x-1)\geq 0\\x\in(-\infty;-4]\cup[\frac{1}{2};+\infty)](/tpl/images/1358/7181/42d33.png)
Пересечём полученные решения: ответом будет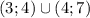
смотри во вложениях...