Алгебра: Какой цифрой оканчивается число 3 в степени 2010?

Какой цифрой оканчивается число 3 в степени 2010?

👇

Ответ:

Leprekon11

22.06.2020

Лично я решил задачу двумя Первый--программа(PascalABC)(она же лёгкий). Второй-- вручную. Дело в том,что тут не нужно считать каждую степень,ведь последними цифрами в числах степеней тройки могут быть только 1,3,7,9.

Я расписал себе на листок 20 первых степеней(точнее даже не степеней,а последних чисел,которые в них получаются. Например,для первых десяти степеней эти числа будут такими:3,9,7,1,3,9,7,1,3,9),увидел последовательность и спокойно проссчитал до 2010 степени.

ответ: 9

4,8(99 оценок)

Открыть все ответы

Ответ:

PolinaDudnik

22.06.2020

Область значений функции - это множество значений, которые может принимать зависимая переменная у при переборе всех х (значений независимой переменной х) из области определения функции. Иными словами, это - та часть оси ординат (оси у), на которой можно найти все значения функции. Область значений обозначается, как E(f).
Например: линейная функция y=ax+b определяется на всей числовой прямой (х∈(-∞;+∞)), значит область значений зависимой переменной у, тоже определяется по всей оси У (E(f)∈(-∞;+∞).
Во вложении, график функции f(x)=2x²+3. Это квадратичная парабола, с ветвями, направленными вверх. По графику видно, что вершина параболы - точка (0;3). Независимая переменная х может принимать любые значения, то есть D(x)∈(-∞;+∞), а минимальное значение функции у=3, значит E(f)=[3;+∞)
При определении области значений функции, нужно обратить внимание на ОДЗ переменной х и есть ли, по условию, ограниченный промежуток значений х (в этом случае, область значений находится только в пределах данного промежутка).
Зависимая переменная у называется так, потому, что она зависит от независимой переменной, которая может принимать любые значения.
Хорошим примером этой зависимости является функция у=а/х. График - гипербола.
При определении х, областью допустимых значений (ОДЗ) является вся числовая прямая, кроме х=0, потому. что на ноль делить нельзя. И, если х не может принять значение 0, то у тоже не может принять значение, соответствующее х=0. И, область значений функции у=а/х, является вся числовая прямая оси У, не включая 0: E(f)∈(-∞;0)∪(0;+∞) - в точке х=0, функция терпит бесконечный разрыв.
Что такое область значений функции?

4,6(72 оценок)

Ответ:

valeriaro294

22.06.2020

Мы имеем ограничения — корни и знаменатель. Проблема в том, что для числителя правой части сложно написать адекватное ОДЗ. А можно ли обойтись без него?

Оказывается, можно. Достаточно записать, что:

$\left \{ {{7-x\geq 0} \atop {x-10}} \right. \Rightarrow x\in(1;7]$

Возведём в квадрат обе части (так как они положительны, имеем право сделать это) и посмотрим, что получится:

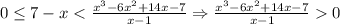
$0\leq 7-x 0$

Дробь положительна, если и числитель, и знаменатель имеют одинаковый знак. По ограничению, которое мы записали выше, знаменатель положителен, значит, числитель обязан быть положительным, то есть это страшное ОДЗ выполняется автоматически. Теперь можно решить получившееся неравенство:

$\frac{x^3-6x^2+14x-7}{x-1}+x-70\\\frac{x^3-6x^2+14x-7+(x-7)(x-1)}{x-1}0\\\frac{x^3-6x^2+14x-7+x^2-8x+7}{x-1}0\\\frac{x^3-5x^2+6x}{x-1}0\\\frac{x(x^2-5x+6)}{x-1}0\\\frac{x(x-2)(x-3)}{x-1}0 \Rightarrow x\in(-\infty;0)\cup(1;2)\cup(3;+\infty)$