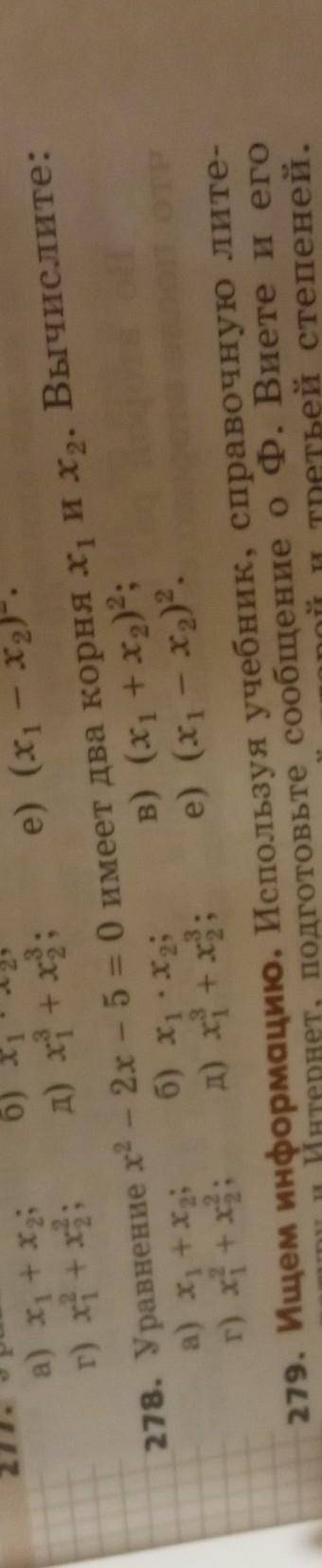
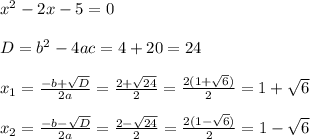
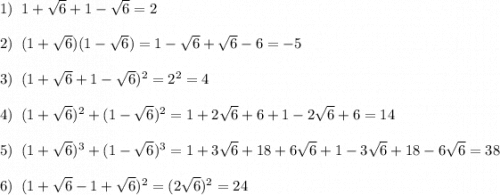
ответ: 12√39 (ед. площади)
Объяснение:
Прямоугольный треугольник с катетами 3 и 4 - египетский, его гипотенуза 5 ( проверьте по т.Пифагора).
Проекция ВС наклонной В1С перпендикулярна СА. По т. о 3-х перпендикулярах В1С⊥СА. Треугольник В1СА - прямоугольный с углом В1АС=60°. В1С=АС•tg60°=4√3. Т.к. призма прямая, боковые ребра перпендикулярны основаниям, поэтому треугольник В1ВС прямоугольный. По т. Пифагора В1В=√(B1C²-BC²)=√[(4√3)²-3²]=√39
Боковое ребро прямой призмы является её высотой, а её боковые грани - прямоугольники.
Площадь боковой поверхности призмы находят умножением её высоты на периметр основания.
S(бок)=В1В•(АВ+ВС+АС)=√39•12=12√39 (ед. площади)
Объяснение:
Во-первых, разберемся с записью.
A - 7/A + 4/B = 1
Предположим, что A стоит отдельно, а в числителе дроби только 7.
При этом мы знаем, что А и В - двузначные числа.
Если даже А = 10, минимальное двузначное число, то получается:
10 - 7/10 + 4/B = 1
4/B = 1 - 10 + 7/10 = -8,3 < 0
Отсюда B < 0, а этого быть не может.
Значит, запись совсем другая:
(A-7)/A + 4/B = 1
То есть в числителе стоит (A-7), а не просто 7. Теперь все понятно:
A/A - 7/A + 4/B = 1
1 - 7/A + 4/B = 1
4/B - 7/A = 0
4/B = 7/A
Это одинаковые дроби, причем с двузначными знаменателями.
Ясно, что если дроби равны, то A > B, потому что 7 > 4.
При этом 10 <= B < A <= 99, так как числа A и B - двузначные.
1) Если A = 21, B = 12, то
4/B = 7/A
4/12 = 7/21 = 1/3.
Наименьшее A = 21.
2) Если A = 98, B = 56, то
4/B = 7/A
4/56 = 7/98 = 1/14.
Наибольшее B = 56.