Правильное условие такое:
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Решение.
ОДЗ: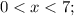 
Методом подбора быстрее.
1) Начнем с решения второго уравнения.
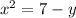
Если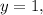 
то 7-1=6. Тогда 
не натуральное число.
Если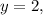 
то 7-2=5. Тогда 
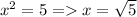не натуральное число.
Если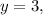 
то 7-3=4. Тогда 
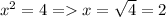натуральное число.
Получили решение
2) Подставим в первое уравнение 
.
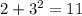
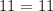верное равенство.
ответ: 2 груши у брата;
3 яблока у сестры.
ответ: Решений в натуральных числах нет
Объяснение:
Пусть : НОД(x,y)= t
x=a*t
y=b*t
a , b взаимно простые натуральные числа.
a^3*t^3 -4*a*t -b^2*t^2=0
a^3*t^2 -b^2*t -4a=0
Очевидно , что b^2 *t делится на a , но поскольку a и b взаимно простые, то t делится на a.
t=m*a
m- натуральное число
a^5 *m^2 -a*b^2*m -4a=0
a^4 *m^2 -b^2*m -4=0
m*( a^4*m -b^2)=4
То есть : m=1 ; 2 ; 4
1) m=1
a^4 -b^2=4
(a^2 -b)*(a^2 +b)=4
Заметим что :
(a^2 -b ) + (a^2+b)=2a^2 - четно , а значит либо обе скобки четны , либо обе нечетны , но тк правая часть делится на 4 , то обе четны .
То есть :a^2-b=a^2+b=+-2
2a^2=+-4
a^2=2
a= sqrt(2) - нецелое число .
Вывод : m=1 не подходит.
2) m=4
4*a^4 -b^2 =1
(2*a^2 -b)*(2*a^2+b)=1
2a^2-b=2a^2+b=+-1
4*a^2=+-2
a^2= 1/2
a=1/sqrt(2) - нецелое число.
3) Основной случай : m=2
2*a^4 -b^2=2
2*(a^4 -1)=b^2
Рассуждения о полных квадратах тут не совсем работают из за назойливой двойки слева. Чтобы от неё избавится ,применим следующий приём:
b^2 - чётно , а значит b так же чётно , то b^2 делится на 4 , а значит:
a^4 -1 четно , а значит a^4 нечетно.
a=2*k-1 k- натуральное число.
2*( a^2-1)*(a^2+1)=b^2
a^2=4k^2-4k+1
2*(4k^2-4k)*(4k^2-4k+2)=b^2
16 * k *(k-1) * ( 2* k*(k-1) +1)=b^2
b^2 делится на 16 , а значит b делится на 4.
b=4*n n- натуральное число
Так же сделаем замену: k*(k-1)=k^2-k =s - целое неотрицательное число.
s*(2s+1)=n^2 , теперь когда мы избавились от осложняющих ситуацию степеней двоек , можно уже начать рассуждать о взаимной простоте. Заметим , что при k>1
k^2-2k+1 < k^2-k<k^2
(k-1)^2<k^2-k <k^2
То есть s находится между двумя соседними квадратами , а значит s не является полным квадратом.
s*(2s+1)=n^2
Тогда если s не полный квадрат , то и 2s+1 не полный квадрат. Очевидно , что при s>0 s и 2s+1 взаимно простые. Действительно , если s делится на некоторое простое число p , то 2*s так же делится на p , но тогда 2s+1 не делится на p. Тк s не является полным квадратом , то оно представляется в виде произведений степеней простых чисел , причём хотя бы одно простое число возведено в нечетную степень .Для 2s+1 ситуация аналогична и в ее состав входят простые множители отличные от s. Таким образом s*(2s+1) неизбежно содержит хотя бы два простых числа возведённых в нечетную степень.
Вывод:
s*(2s+1) не является полным квадратом при s>0
Пусть s=0 , но тогда b=0 , то y=0 что не является натуральным числом.
Вывод: уравнение не имеет решений в натуральных числах.
P.S Скажу теперь ,почему нельзя рассуждать про квадраты в выражении: (обязательно кто нибудь спросит)
2*(a^4-1)=b^2
Безусловно и понятно , что a^4 -1 (при a >1) не полный квадрат и казалось бы это значит , что 2*(a^4-1) сразу же не является полным квадратом. Но на самом деле это так сразу далеко не очевидно! Ведь разложение на простые четного числа a^4 -1 ,не являющего квадратом , может содержать нечетную степень двойки , а все остальные степени простых чисел буду четны . В этом смысле все таки остаётся вероятность ,что 2*(a^4-1) может быть полным квадратом. Кому то может показаться ,что простая двойка никак не может осложнить жизнь , но это большое заблуждение!
5х^2-8х-4=0
Д=64-4*5*(-4)=12^2
х=(8+-12)/10
х1=2 х2=-0,4
(2+(-0,4))/2=0,8