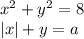
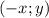, то будет 
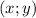. Это возможно когда 
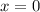. Система примет вид 
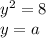, так как второе это уравнение симметрично относительно друг - другу прямые . То ответом будет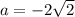 
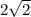. Второе уравнение начало которых совпадает двух прямых , симметричные относительно друг друга .
должно быть максимальным , то ясно что оно должно быть таким что , при проведений через эту точку , две прямые были касательные к окружности . 
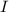четверть координатной плоскости. Получим прямоугольный равнобедренный треугольник , с катетами тогда 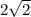должно быть высотой . То есть выполняется условие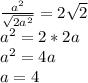 
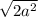- это гипотенуза данного треугольника
Чтобы избавиться от модуля, нужно рассмотреть два случая: когда выражение под знаком модуля неотрицательно (и тогда это модуль равен самому этому выражению), и когда выражение под знаком модуля отрицательно (и тогда это модуль равен выражению, взятому с обратным знаком).
1. Выражение под знаком модуля приравниваем нулю и решаем получившееся уравнение, чтобы узнать интервалы, на которых это выражение может менять свой знак.
х-4=0 → х=4.
2. Рассматриваем случай х<4
При этом выражение отрицательно, следовательно |x-4| = 4-x
-3|x-4|-x = -3(4-x)-x = -12+3x-x = 2x-12 = 2(x-6)
3. Рассматриваем случай x≥4
При этом выражение неотрицательно, поэтому |x-4| = х-4
-3|x-4|-x = -3(x-4)-x = -3x+12-x = -4x+12 = 4(3-x)
4. Объединяя два эти выражения, получаем