Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2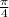
) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.
Велосипедист и мотоциклист, двигаясь навстречу друг другу, находились в пути: 14-10=4(час)
Отсюда скорость сближения велосипедиста и мотоциклиста равна:
Vсближ.=S/t
V=176:4=44 (км/час)
Скорость сближения, при движении навстречу друг другу, равна сумме скоростей велосипедиста и мотоциклиста., поэтому обозначив скорость
велосипедиста за (х) км/час, скорость мотоциклиста равна (44-х) км/час.
Если бы велосипедист выехал в 13 часов , то до 14 часов, он потратил бы время в пути:
14-13=1 (час), а расстояние, которое он проехал бы составляло: х*1 (км), если бы мотоциклист выехал в 9 часов, то до 14 часов, он потратил бы время в пути:
14-9=5 (час), а расстояние, которое он проехал бы составляло:
(44-х)*5 (км)
А так как общее расстояние , которое бы проехали велосипедист и мотоциклист составляло бы: 176-8=168 (км)
На основании этого составим уравнение:
1*х+(44-х)*5=168
х+220-5х=168
х-5х=168-220
-4х=-52
х=-52:-4
х=13 (км/час) - это скорость велосипедиста
Скорость мотоциклиста равна:
44-13=31 (км/час)
ответ: Скорость мотоциклиста равна 31 км/час