Полное условие смотри в приложении.
а)
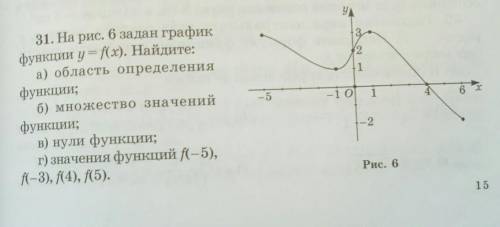
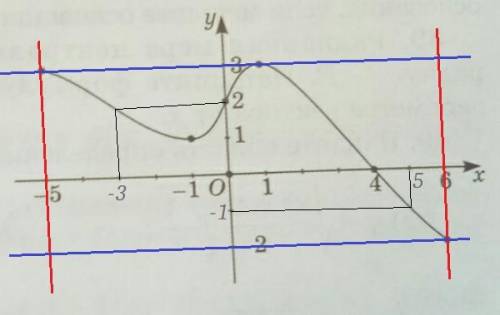
На графике область определения это множество значений, которые принимают x, для этого графика. Видно, что -5 ≤ x ≤ 6.
ответ: D(f) = [-5;6].
б)
Множеством значений, будет множество для y. -2 ≤ y ≤ 3.
ответ: E(f) = [-2;3].
в)
Нули функции это координата точки пересечения графика с осью Ox, по оси Ox. Точка: (4;0), координата по оси Ox: 4.
ответ: x = 4.
г)
Необходимо найти значение (y) функции f(x) для данных аргументов (x). Определяем точку графика с соответствующим x, а затем находим для неё y.
ответ: f(-5) = 3; f(-3) = 2; f(4) = 0; f(5) = -1.
2)Аналитически
По-моему мнению, решая неравенства, самый рациональный через тригонометрический круг. Но мы разберем сразу 2 варианта.
№1. Тригонометрический круг
Как мы помним, на круге отсчитываем синус по игреку. Ищем значение 1/2, и проводим хорду так, чтобы она проходила через точку 1/2 (по игреку, напомню еще раз). То, что ниже этой хорды и будут решениями неравенства. Нетрудно сообразить, что sin30 градусов даст 1/2. Но и sin150 градусов даст 1/2. Таким образом, отсюда вытекает двойное неравенство:
150<sinx<30
P.S. Все, что я обвел желтым - это решение данного неравенства (рис. 1)
№2. Аналитический
Рассмотрим уравнение:
Решая уравнение, получим:
Чтобы неравенство было верным, нужно, чтобы угол альфа был меньше, или равен корням уравнения sinx=1/2.
Опять же, отсюда вытекает двойное неравенство:
150<sinx<30