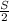м, тогда и вторая половина трассы будет иметь длину 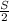м. Найдем час, за который автомобиль проехал первую половину трассы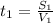 
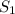- длинна первой половины трассы 
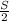м.
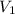- скорость на первой половине трассы 
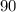км/ч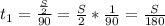
час за который автомобиль первую половину трассы.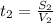
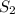-вторая половина трассы - 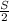м.
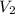- скорость на второй половине трассы 
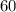км/ч.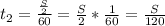
час за который автомобиль проехал вторую половину трассы.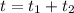
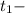
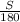
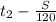
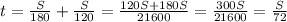
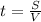
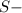длинна всей трассы, у нас получилась 
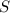м.
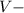скорость автомобиля на всей трассе, или средняя скорость.Получается что средняя скорость автомобиля на протяжении всего пути была 
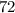км/ч.
Для решения примеров нужно воспользоваться формулами сокращенного умножения, в частности формулой разности квадратов: a² - b² = (a - b)(a + b).
1) (a + 2b)² - (3c + 4d)² = (a + 2b - 3c - 4d)(a + 2b + 3c + 4d);
2) (m - 2n)² - (2p - 3q)² = (m - 2n - (2p - 3q))(m - 2n + 2p - 3q) = (m - 2n - 2p + 3q)(m - 2n + 2p - 3q);
3) 9(m + n)² - (m - n)² = (3(m + n))² - (m - n)² = (3(m + n) - (m - n))(3(m + n) + m - n) = (3m + 3n - m + n)(3m + 3n + m - n) = (2m + 4n)(4m + 2n) = 2(m + 2n) · 2(2m + n) = 4(m + 2n)(2m + n);
4) 16(a + b)² - 9(x + y)² = (4(a + b))² - (3(x + y))² = (4a + 4b - (3x + 3y))(4a + 4b + 3x + 3y) = (4a + 4b - 3x - 3y)(4a + 4b + 3x + 3y).