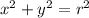 , задаёт окружность радиуса r
, задаёт окружность радиуса r
Что бы задать лучи, используем несколько функций вида 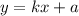
При a = 0, все прямые, задаваемые уравнениями вида 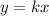 , будут проходить через точку пересечения координатных осей.
, будут проходить через точку пересечения координатных осей.
Возьмём 5 прямых, которые будут иметь угол с осью Ох, соответственно, в 0, 30, 60,120, 150 градусов. Этим углам соотвествуют следующие значения углового коэффициента k: 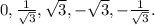 Под углом 90 градусов будет падать прямая x = 0.
Под углом 90 градусов будет падать прямая x = 0.
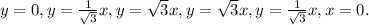
Осталось вырезать у этих прямых отрезки, которые лежат внутри окружности. Для этого найдём точки пересечения этих прямых и окружности.
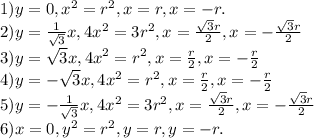
Тогда:
![(x^2+y^2 = r^2) \cup (y=0, x \in (-\infty, -r]\cup[r, +\infty)) \cup\\ (y=\frac{1}{\sqrt{3}}x, x \in (-\infty, -\frac{\sqrt{3}r}{2}]\cup[\frac{\sqrt{3}r}{2}, +\infty))\cup\\(y=\sqrt{3}x, x \in (-\infty, -\frac{r}{2}]\cup[\frac{r}{2}, +\infty))\cup\\(y=-\sqrt{3}x, x \in (-\infty, -\frac{r}{2}]\cup[\frac{r}{2}, +\infty)\cup\\(y=-\frac{1}{\sqrt{3}}x, x \in (-\infty, -\frac{\sqrt{3}r}{2}]\cup[\frac{\sqrt{3}r}{2}, +\infty))\cup\\(x=0, y \in (-\infty, -r]\cup[r, +\infty))](/tpl/images/0155/2774/da10b.png)
ctgx(ctgx+1)=0
ctgx=0 или ctgx+1=0
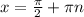 ctgx=-1
ctgx=-1
n=-1 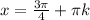
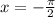 k=-1
k=-1
n=0 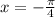
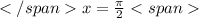 k=0
k=0
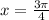
т.е. на данном промежутке находятся 4 корня
1)Ира не помгла принести 43 и 34 яблока,так как если в каждом пакете по 5 яблок,общее число должно делиться на 5. 55 яблок она погла принести 55:5=11пакет с 55 яблоками принесла.
2) хпачек упаковывает 1
х+2 пачек упаковывает 2
всего за 30 мин упакуют (х+х+2)*30=600
х+х+2*30=600
2х+2=20
2х=18
х=9 пачек в минуты упаковывает 1
9+2=11 пачек упаковывает 2
ответ: 9;11
3) Чтобы узнать можно лисделать 3 подарка,нужно числа поделить на 3,чтобы число получилось без остатка.
Значит 3 одинаковых подарка можно, а 9и 2 нельзя,так как числа 129,102,186 поделятся на них с остаткой,чего быть не должно.
Совокупность таких уравнений определит лучики солнышка:
у=1/2*x
y=x
y=2x
y=-2x
y=-x
y=-1/2*x
: