Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру уравнение в действительных корнях.
Рассмотрим функцию . Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Ой, сложный график. Я давно такие не решала. Ну это как я думаю. Сначала тебе нужно раскрыть модули. Нужно рассматривать два случая , когда x>или равно 0 и x<0 Раскрываем. y=|x|*x+|x|-3x 1)x>или рано 0 y=x^2+x-3x y=x^2-2x график -парабола , ветви вверх Найдём вершину параболы X=-b/2a X=2/2=1 y=-1 (1;-1)-вершина параболы Составляем таблицу Только составь правильно Нельзя брать отрицательные значения. Обязательно нужно взять 1. Чтобы графики совпадали. Берёшь 1,2,3,4,,5 подставляешь в уравнение и находишь y. Чертишь первую параболу 2)y=-x^2-x-3x x<0 Y=-x^2-4x График-парабола , ветви вниз Находим вершину X=4/2=2 Y=-4-4=-8 (2;-8) Составляешь таблицу . Только нужно учесть , что x<0 То есть берём отрицательные значения и нуль. Не забудь взять 1. Чтобы графики соприкасались. 1,0,-1,-2,-3,-4. Подставляешь и находишь y. Чертишь график. Тааак. Теперь нужно найтиy=m 2 общих. Ведёшь линейкой с низу вверх . И смотришь где есть 2 общие точки. Находишь и от x, считаешь вверх или вниз сколько получается. Это и будет y=m.
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру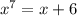 уравнение в действительных корнях.
уравнение в действительных корнях.
Рассмотрим функцию . Эта функция является возрастающей на всей числовой прямой.
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.