Выделите квадрат двучлена.
Объяснение:
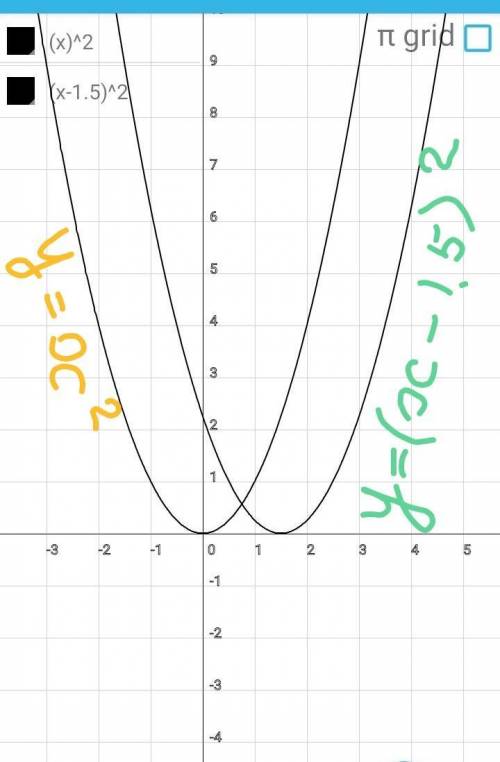
1.
у=х^2-3х+1=(х^2-2×1,5х+1,5^2)-1,25=
=(х-1,5)^2-1,25
Строим график:
Шаг 1:
Строим график у=х^2.
Шаг 2:
Параболу перемещаем вдоль ОХ впра
во на 1,5ед.
Шаг 3:
Совершаем параллельный перенос
вдоль ОУ вниз на 1,25ед.
Построен искомый график.
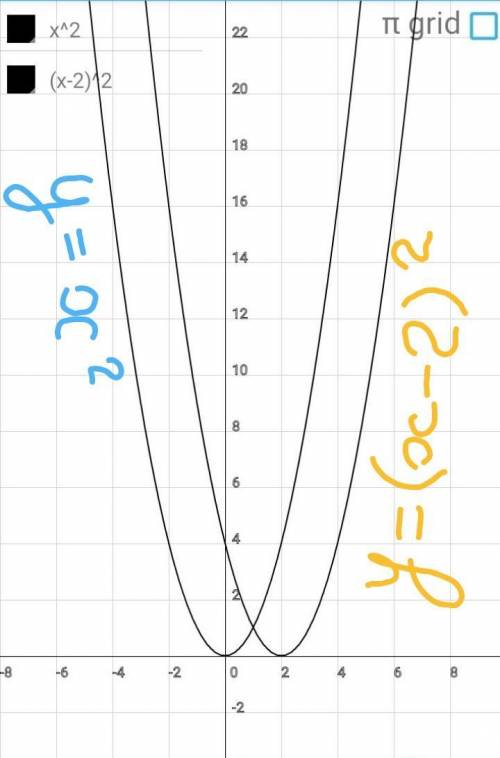
2.
у=-х^2+4х+2
у=-(х^2-2×2х+2^2)+6=
=-(х-2)^2+6
Строим график:
Шаг 1:
Строим график у=х^2
Шаг 2:
Параболу перемещаем вдоль ОХ
вправо на 2ед. (ветви направлены
вверх).
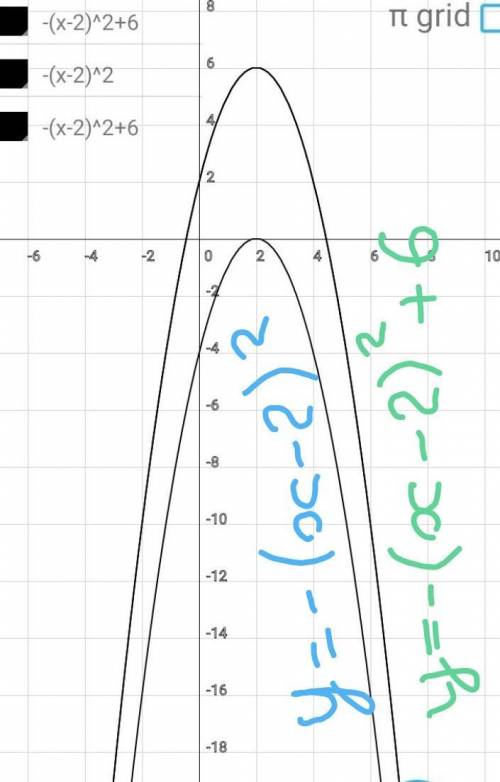
Шаг 3:
Отражаем зеркально относитель
но ОХ (ветви параболы идут вниз).
Шаг 4:
Совершаем параллельный пере
нос вдоль ОУ вверх на 6ед.
Искомый график построен.


Выделите квадрат двучлена.
Объяснение:
1.
у=х^2-3х+1=(х^2-2×1,5х+1,5^2)-1,25=
=(х-1,5)^2-1,25
Строим график:
Шаг 1:
Строим график у=х^2.
Шаг 2:
Параболу перемещаем вдоль ОХ впра
во на 1,5ед.
Шаг 3:
Совершаем параллельный перенос
вдоль ОУ вниз на 1,25ед.
Построен искомый график.
2.
у=-х^2+4х+2
у=-(х^2-2×2х+2^2)+6=
=-(х-2)^2+6
Строим график:
Шаг 1:
Строим график у=х^2
Шаг 2:
Параболу перемещаем вдоль ОХ
вправо на 2ед. (ветви направлены
вверх).
Шаг 3:
Отражаем зеркально относитель
но ОХ (ветви параболы идут вниз).
Шаг 4:
Совершаем параллельный пере
нос вдоль ОУ вверх на 6ед.
Искомый график построен.





(9; 24).
Объяснение:
у= 4х-12 и у=2х+6
1) Найдём абсциссу точки пересечения графиков:
4х - 12 = 2х + 6
4х - 2х = 12 + 6
2х = 18
х = 18 : 2
х = 9
2) Найдём ординату точки пересечения:
если х = 9, то у = 2•9 + 6 = 18 + 6 = 24.
(9; 24).