7
Объяснение:
х - количество станков в день по плану (плановая производительность),
(х + 2) - количество станков в день на самом деле (реальная производительность),
 - время изготовления 35 станков по плану (в днях),
- время изготовления 35 станков по плану (в днях),
35 + 7 = 42 (ст.) - количество станков, которые изготовил завод.
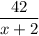 - время изготовления 42 станков.
- время изготовления 42 станков.
Время по плану на 1 день больше реального. Составим уравнение:
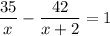
35(x + 2) - 42x = x(x + 2)
35x + 70 - 42x = x² + 2x
x² + 9x - 70 = 0
D = 81 + 280 = 361
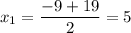
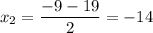 - не удовлетворяет условию
- не удовлетворяет условию
х + 2 = 5 + 2 = 7 станков в день изготовлял завод.
Сначала определим значение а из второго уравнения, для чего подставим в него заданные корни (5;-3):
a * x + 3 * y = 11;
a * 5 + 3 * ( - 3) = 11;
a * 5 - 9 = 11;
а * 5 = 11 + 9;
а * 5 = 20;
а = 20/5;
а = 4.
Теперь можно записать заданную систему в нормальном виде:
1) 5 * x + 2 * y = 12;
2) 4 * х + 3 * у = 11.
Умножим 1) на 3, а 2) на 2:
1_1) 15 * x + 6 * y = 36;
2_1) 8 * х + 6 * у = 22.
Теперь вычтем из 1_1) уравнение 2_1):
15 * x + 6 * y - 8 * х - 6 * у = 36 - 22;
15 * x - 8 * х + 6 * y - 6 * у = 36 - 22;
7 * х = 14;
х = 14/7;
х = 2.
Выразим у из 1):
5 * x + 2 * y = 12;
2 * y = 12 - 5 * x;
у = 6 - 2,5 * х.
Подставим х = 2:
у = 6 - 2,5 * 2 = 1.
ответ: (2; 1).
Объяснение:
Сначала определим значение а из второго уравнения, для чего подставим в него заданные корни (5;-3):
a * x + 3 * y = 11;
a * 5 + 3 * ( - 3) = 11;
a * 5 - 9 = 11;
а * 5 = 11 + 9;
а * 5 = 20;
а = 20/5;
а = 4.
Теперь можно записать заданную систему в нормальном виде:
1) 5 * x + 2 * y = 12;
2) 4 * х + 3 * у = 11.
Умножим 1) на 3, а 2) на 2:
1_1) 15 * x + 6 * y = 36;
2_1) 8 * х + 6 * у = 22.
Теперь вычтем из 1_1) уравнение 2_1):
15 * x + 6 * y - 8 * х - 6 * у = 36 - 22;
15 * x - 8 * х + 6 * y - 6 * у = 36 - 22;
7 * х = 14;
х = 14/7;
х = 2.
Выразим у из 1):
5 * x + 2 * y = 12;
2 * y = 12 - 5 * x;
у = 6 - 2,5 * х.
Подставим х = 2:
у = 6 - 2,5 * 2 = 1.
ответ: (2; 1).
(9x-15y+26z)-(-16x+26y-16z)=
9x-15y+26z+16x-26y+16z=
25x-41y+42z