Question

Сложить дифференциальное уравнение и решить его найти кривую, которая проходит через точку (2; 2) и, в которой точка пересечения любой ее касательной с осью ox одинаково отдалена от точки касания и точки (0; 0) с подробным решением

Answer 1

Уравнение касательной: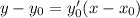 $y-y_0=y'_0(x-x_0)$

Отсюда: точка касания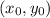 $(x_0,y_0)$;

точка пересечения с осью Ох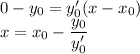 $0-y_0=y'_0(x-x_0)\\ x=x_0-\dfrac{y_0}{y'_0}$

Расстояние от точки (0,0) до точки пересечения с осью Ох, конечно, равно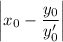 $\left|x_0-\dfrac{y_0}{y'_0}\right|$

Расстояние от точки касания до точки пересечения с осью Ох:

$\sqrt{(y_0-0)^2+\left(x_0-\left(x_0-\dfrac{y_0}{y'_0}\right)\right)^2}=\sqrt{y_0^2+\dfrac{y_0^2}{y'_0^2}$

$\left|x_0-\dfrac{y_0}{y'_0}\right|=\sqrt{y_0^2+\dfrac{y_0^2}{y'_0^2}}\\ x_0^2-\dfrac{2x_0y_0}{y'_0}+\dfrac{y_0^2}{y'_0^2}=y_0^2+\dfrac{y_0^2}{y'_0^2}\\ x_0^2-\dfrac{2x_0y_0}{y'_0}=y_0^2\\ y'_0=\dfrac{2x_0y_0}{x_0^2-y_0^2}$

Перепишем в приличном виде:

$y'=\dfrac{2xy}{x^2-y^2}$

Положим y=xv, тогда y'=xv'+v:

$xv'+v=\dfrac{2x^2v}{x^2-x^2v^2}\\ xv'=\dfrac{2v}{1-v^2}-v=\dfrac{v^3+v}{1-v^2}\\$

Это простейшее уравнение с разделяющимися переменными, решим его:

$\dfrac{1-v^2}{v^3+v}dv=\dfrac{dx}{x}\\ \int\dfrac{1-v^2}{v^3+v}dv=\ln Cx$

$\dfrac{1-v^2}{v(1+v^2)}=\dfrac1v-\dfrac{2v}{1+v^2}$

$\int\dfrac{1-v^2}{v(1+v^2)}=\ln|v|-\ln(1+v^2)$

$\dfrac{v}{1+v^2}=Cx\\ \dfrac{y/x}{1+y^2/x^2}=Cx\\ \dfrac{y}{x^2+y^2}=C$

Это уравнение задает семейство окружностей с центром на оси ординат, проходящих через точку (0,0).

Учитывая, что окружность должна проходить через точку (2,2), находим значение С:

$C=\dfrac{2}{4+4}=\dfrac14$

ответ. это окружность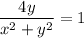 $\dfrac{4y}{x^2+y^2}=1$.

P.S. На самом деле, то, что должна получаться окружность, практически очевидно. Условие равенства отрезков касательной, проведенных из одной точки, известно еще из школьного курса геометрии. 

P.P.S. На досуге можно подметить, что в точке (2,2) производная бесконечна, и в дифуре можно (?) найти некоторую неоднозначность...