3/8
Объяснение:
Поскольку числитель на 5 меньше знаменателя, дробь имеет вид
x-5--. x
Если числитель этой дроби уменьшить на 2, а знаменатель увеличить на 16, то получится дробь
x-7--. x+16
Получаем уравнение
x-5 x-7 1 - - = - - + -. xx+16 3
Домножив обе части этого равенства на 3x (x+16) и преобразовав, получаем квадратное уравнение:
3 (x-5) (x+16) = 3 (x-7) x+x (x+16),
3 (x²+11x-90) = 3x²-21x+x²+16x,
x²-38x+240=0.
Дискриминант D=38²-4·240=484=22², корни x = (38±22) / 2=30 и 8. Этим корням соответствуют две дроби
25 3 - и -.30 8
Первая сократимая, вторая несократимая.

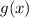 ;
; ;
; и будет искомой фигурой.
и будет искомой фигурой.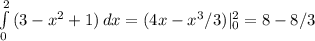
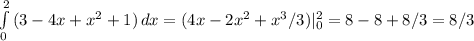
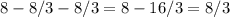 (кв. ед.)
(кв. ед.)
только первое решение