а- первый член прогрессииd - разность прогрессии а2+а5=а+d+а+4d=2a+5da2*a3=(a+d)(a+2d)=a^2+da+2da+2d^2 Получаем систему уравнений:2a+5d=18a^2+3ad+2d^2=21 Выразим из первого уравнения а:a=(18-5d)/2=9-2,5d Подставим во второе уравнение:(9-2,5d)(9-2,5d)+3(9-2,5d)d+2d^2-21=0 Когда раскроем все скобки и сведем все члены, получим квадр. уравнение вида:0,75d^2-18d+60=0 Решив это уравнение, получим 2 корня d=20 и d=4d=20 - не подходит,т.к. получается, что второй член не является натуральным числом (-21), что противоречит условию. Подставим d=4 в первое уравнение:2а+20=182а=-2а=-1 ответ: а1=-1, d=4.
Любое нечётное число можно записать в виде 2n-1, где n∈z (множество целых чисел). у нас три последовательных нечётных числа. каждое последующее нечётное число на 2 больше предыдущего (например, 1, 3, 5, 7 и так далее). обозначим минимальное из наших чисел 2n-1. тогда следующее будет 2n-1+2=2n+1, а последнее 2n+1+2=2n+3. эти числа в порядке возрастания расположатся, очевидно: 2n-1; 2n+1; 2n+3. по условию : (2n+1)(2n+-1)(2n+1)=76 (2n+1)(2n+3-(2n-=0 (2n+1)(2n+3-2n+1)-76=0 (2n+1)4-76=0 8n+4-76=0 8n-72=0 n=72/8 n=9 тогда искомые числа будут: 2n-1=2*9-1=18-1=17 2n+1=2*9+1=18+1=19 2n+3=2*9+3=18+3=21
Объяснение:
2 - Б
3.
А - 2
Б - 1
4.
5. знаменатель не должен быть равен 0
2х+7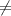 0
0
х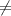 -7
-7
х ≠ -3.5