
Итак, есть уравнение

Сразу накладываем ограничение на знаменатель: 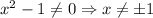
Ситуация, когда у заданного в условии уравнения всего 1 корень, это когда 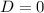 у числителя, и этот корень не равен ни одному из двух значений из нулей знаменателя или же когда
у числителя, и этот корень не равен ни одному из двух значений из нулей знаменателя или же когда 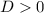 , но один из корней (именно один) равен одному из двух значений из нулей знаменателя дроби, тогда это значение корнем уравнения являться не будет и благополучно останется другой корень.
, но один из корней (именно один) равен одному из двух значений из нулей знаменателя дроби, тогда это значение корнем уравнения являться не будет и благополучно останется другой корень.
Решим уравнение 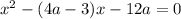
Это квадратное уравнение, и что-то мне подсказывает, что дискриминант в нем будет полным квадратом.
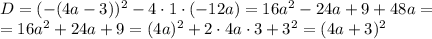
Впрочем, неудивительно. Для решения квадратного уравнения берется корень, здесь корень из квадрата, да, формально это модуль, но именно при решении квадратных уравнений модуль можно опустить, потому что при объединении всех решений с раскрытия модуля как раз все нормально получается, поэтому его сразу опустим.
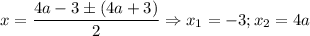
Вообще прекрасно, один корень это число, причем которое не входит в нули знаменателя. Ситуация, когда -3 - единственный корень будет при 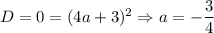
Осталось проверить, когда 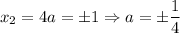
Теперь запишем ответ, как требуется, по возрастанию десятичные числа через пробел.
ответ: -0.75 -0.25 0.25
При каких значениях параметра уравнение (x²-(4a-3)x -12a ) / (x²-1) =0 имеет 1 корень .
Решение : (x² - (4a - 3)x - 12a ) / (x² - 1 ) = 0 ⇔
{ x²-(4a-3)x -12a = 0 ;
{x² - 1 ≠ 0 . || ОДЗ ||
x²- 1≠ 0⇔x ≠ ± 1 * * * (x+1)(x-1) ≠0⇔ x+1≠0 и x-1 ≠0 ⇔ x ≠ -1 и x ≠ 1 * * *
x² - (4a - 3)x - 12a = 0
- - -
Если a =0 * * * - 12a = 0 * * *
x²-(4a-3)x-12a =0 ⇔x² +3x=0⇔(x+3)x=0⇒x₁ = -3,x₂= 0 два корня
- - -
D=(4a-3)²- 4*1*(-12a) =16a²-24a +9-4*1*(-24a)=16a²+24a+9 = (4a+3)² ≥0
Если D = 0 ⇔ 4a+3=0⇔ a = - 3/4 x₁=x₂=(4a-3)/2 = - 3 ( кратный корень)
По уставу ЕГЭ _ одно решение
звучит так: Квадратное уравнение имеет ОДИН корень, если D=0
* * * a = - 3/4 ⇒x²- (4a-3)x -12a =0 ⇔ x²+6x+9 =0 ⇔(x+3)² = 0 ⇒x = -3 * * *
x₁,₂ = (4a-3 ±(4a+3) ) /2 ;
x₁ =(4a-3- 4a- 3) /2 = -3 ; ясно x₁ = -3 решение ( ∈ ОДЗ )
* * * уже обеспечен один корень * * *
x₂=(4a-3 +4a+3)/2 = 4a
Для того чтобы уравнение имел только один корень x₂=4a не должно быть корнем , т.е. 4a = - 1 или 4a = 1 . a = - 1/4 или a = 1 /4
* * * [ 4a = - 1 ; 4a = 1 . ( совокупность уравнений ) * * *
ответ: - 3/4 -1/4 ; 1/4 . * * * -0,75 ; - 0,25 ;0,25 * * *
* * * P.S. Квадратное уравнение ax²+bx+c =0 ⇔a(x+b/2a)²- D/4a =0 ;a≠0 .
если D = 0 , то ( x+b/2a)² = 0 ⇒ x₁ = x₂= - b/2a_двукратный корень * * *